Подкоренное выражение корня чётной степени должно быть неотрицательным, то есть ≥ 0 , но второй корень находится в знаменателе, а знаменатель не должен равняться нулю, так как на ноль делить нельзя. Следовательно подкоренное выражение корня, находящегося в знаменателе, должно быть строго больше нуля.
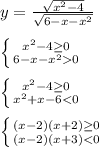
+ - +
1) ___________[-2]__________[2]_________
//////////////////////////// ////////////////////
+ - +
2)______(-3)_______________(2)_________
///////////////////////////////////
ответ : x ∈ (-3 ; - 2]
2. Проводим вторую диагональ получившегося прямоугольника.
3. Получилось четыре одинаковых прямоугольных треугольника.
4. Разбиваем прямоугольник на четыре равных прямоугольника проводя параллельные прямые через точку пересечения диагоналей.
5. Получившиеся прямоугольники имеют наибольшую площадь так как в сумме дают полную площадь прямоугольника.
6. Площадь прямоугольника 8*5=40 см².
7. Площадь вписанного прямоугольника 40/4=10 см².