х - скорость течения
18+х - скорость катера по течению
Общее время= время по реке+время по озеру=40мин:60=2/3час
10/ 18+х + 3/18 =2/3
10/ 18+х + 3/18 - 2/3 =0
10/ 18+х + 1/6 - 2/3 =0
Приведём к общему знаменателю: (18+х)*6*3
180+54+3х-216-2х=0 (18+х)*6*3≠0
18-9х=0 х≠-18
-9х=-18
х=2 км/час - скорость течения реки
ответ: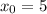 
.
Угловой коэффициент прямой у=2х-2 равен k=2 . Если касательная параллельна этой прямой или совпадает с ней , то их угловые коэффициенты равны.
Угловой коэффициент касательной к графику функции y=f(x) равен значению производной в точке касания, то есть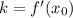 
.
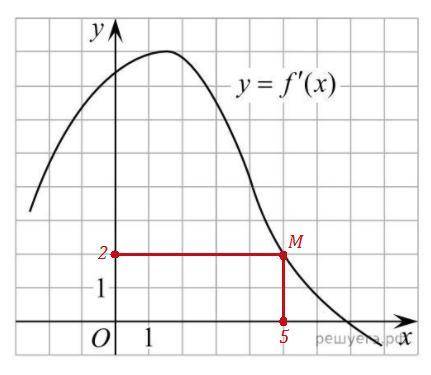
На оси ординат находим значение у=2, проводим прямую, параллельную оси ОХ, и находим на графике функции точку М - точку пересечения графика с прямой у=2.
Далее Находим абсциссу точки М . Это и будет абсцисса точки, в которой касательная к графику функции y=f(x) параллельна прямой y=2x-2 или совпадает с ней.
Координаты точки М(5;2) , значит .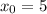
Скорость лодки в неподвижной реке равна 15 км/ч.
Объяснение:
Пусть скорость лодки в неподвижной воде - х.
Для решения этой задачи нам требуется составить уравнение и решить его.
v(реки) = v(плота) = 3 км/ч. 48 км / 3 км/ч = 16 (ч) - плыл плот;
16 ч - 1 ч = 15 (ч) - плыла лодка (так как она отправилась через час, из условий).
Выходит уравнение:
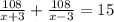Решаем его:
108(x - 3) + 108(x + 3) - 15(x - 3)(x + 3) = 0, где x ≠ 3 и х ≠ -3. <=>
108x - 324 + 108x + 324 - 15x² + 135 = 0
-15x² + 216x + 135 = 0
5x^2 - 72x - 45 = 0
D = 5184 + 900 = 6084. √D = √6084 = 78.
x₁ = (72 - 78) / 10 - не подходит по условию задачи
x₂ = (72 + 78) / 10 = 15 км/ч.
Мы за х взяли скорость в неподвижной реке, значит, х = 15 км/ч - это и есть ответ.
Возьмем скорость катера за U₁, а скорость течения за U₂.
По реке:
S = 10 км.
U = U₁+U₂ = 18+U₂ км/ч
По озеру:
S = 3 км.
U = U₁ = 18 км/ч
tобщее = t₁+t₂ = 40 м. = ⅔ ч.
Составляем уравнение:
⅔ = 10/18+U₂ + 3/18
10/18+U₂ = 4/6 - 1/6 = 3/6 = 1/2
U₂ = 10*2-18 = 2км/ч