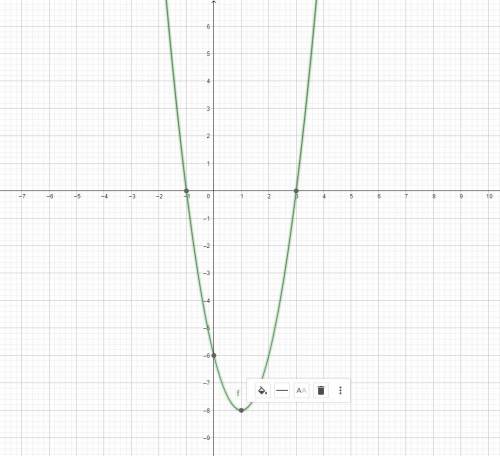
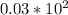Я прикрепил фото того, как выглядит график. А сейчас разберемся как его строить.
Для начала давай раскроем скобки:
y = (2x - 6)(x + 1) //внесли двойку
y = x*(2x - 6) + (2x - 6) //раскрыли вторую скобку
y = 2x^2 - 6x + 2x - 6
y = 2x^2 - 4x - 6
Теперь можно решать по разному. Если хочешь напишу ещё
А пока воспользуемся самым действенным
Примем x0 и y0 за координаты вершины параболы.
Тогда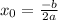 
, а 
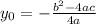(вторую формулу если что можно не запоминать, можешь просто подставить в уравнение полученное x0)
И так
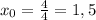
Значит
Теперь может просто подставлять значения. Но в данном случае можешь схитрить.
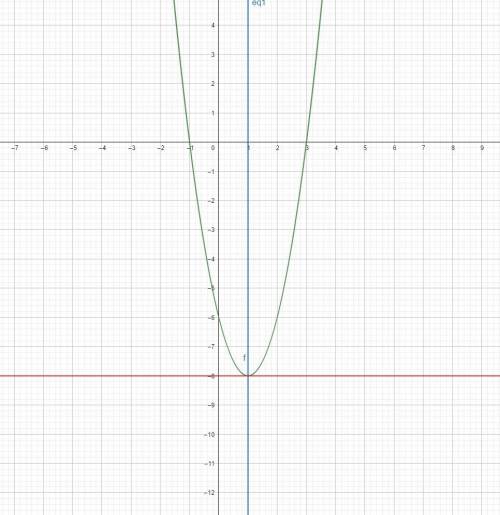
Так как изначальное уравнение выглядело как y = 2(x - 3)(x + 1), то если присмотреться, то можно заметить, что эта парабола пересекает ось x в точках 3 и -1. Но самое интересное это коэффициент 2. Ты можешь просто квадраты x умножать на два и получать желанную точку. После просмотра второй картинки, мои слова станут более понятны
#1. |2x-3|=3-2x, если х<3/2; |2x-3|=2x-3, если х≥3/2;
|x-2|=2-x, если х<2; |x-2|=-2x, если х≥2;
|x-6|=6-x, если х<6; |x-6|=x-6, если х≥6.
Получаем три случая:
1) на множестве (-∞;3/2)U[2;6) получаем неравенство
(2х-3)(х-2)≥(6-х)+2
2х²-3х-4х+6-6+х-2≥0
2х²-6х-2≥0
х²-3х-1≥0
D=9+4=13
![(x-\frac{3-\sqrt{13}}{2})(x-\frac{3+\sqrt{13}}{2})\geq0 \\\ x \in (-\infty; \frac{3-\sqrt{13}}{2}] \cup [\frac{3+\sqrt{13}}{2}; +\infty)](/tpl/images/0172/7524/775a9.png)
C учётом (-∞;3/2)U[2;6) получим ![x \in (-\infty; \frac{3-\sqrt{13}}{2}]](/tpl/images/0172/7524/fc8b3.png)
2) на интервале 1,5≤х<2 получим неравенство
(2х-3)(2-х)≥(6-х)+2
4х-6-2х²+3х-6+х-2≥0
-2х²+8х-14≥0
х²-4х+7≤0
D=16-28<0
решений нет
3) на интервале х≥6 получим неравенство
(2х-3)(х-2)≥(х-6)+2
2х²-3х-4х+6+6-х-2≥0
2х²-8х+10≥0
х²-4х+5≥0
D=16-20<0
решений нет
ответ:
#2. Пусть ∆АВС-прямоугольный треугольник с гипотенузой АВ, катетами АС и ВС.
По условию ВС+АВ=11, tg В = 3/4.
По определению тангенса острого угла прямоугольного треугольника
tg B=AC/BC=3/4 => 3BC=4AC =>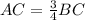 
По теореме Пифагора АВ² = АС² + ВС²
Пусть ВС=х, тогда АВ=11-х, АС=3х/4
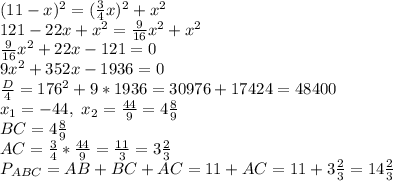
ответ: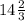 
Стандартный вид числа выглядит так:
3 в стандартном виде будет выглядеть так:
3 =