По условию необходимо найти числа, кратные 5. Значит, последней цифрой искомых чисел может быть 0 или 5.
1. В первом случае, когда число заканчивается цифрой 0, остальные 4 цифры можно выбирать из множества девяти цифр {1,2,3,...8,9}.
В решении используем размещения, так как порядок элементов важен, ведь поменяв местами цифры, числа изменятся.
Размещением из n элементов по m элементов (m≤n) называется упорядоченная выборка элементов m из данного множества элементов n.
Размещения вычисляются по формуле Amn=n!(n−m)!
По формуле получим число вариантов A49=9!(9−4)!=3024
2. Если число oканчивается цифрой 5, то в качестве первой цифры можно взять любую из восьми цифр 1,2,3,4,6,7,8,9 — нельзя использовать 0, т.к. число должно быть 5-значным.
Цифры со второй по 4 можно выбрать A38=8!(8−3)!=336 различными Следовательно, по правилу произведения имеется 8⋅A38 чисел, оканчивающихся цифрой 5.
По правилу суммы находим, сколько существует чисел, удовлетворяющих условию задачи A49+8⋅A38=3024+8⋅336=5712
ответ: 5712
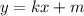 : если k>0, функция возрастает, k<0 - убывает. Всё просто. Т.е. в убывании обе функции линейные, k<0 и в первом (k=-7), и во втором
: если k>0, функция возрастает, k<0 - убывает. Всё просто. Т.е. в убывании обе функции линейные, k<0 и в первом (k=-7), и во втором 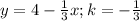 . С этим разобрались. Теперь к возрастанию. Я не знаю, в каком Вы классе, постараюсь объяснить доступно. Чтобы определить возрастание/убывание функции, нужно взять значения
. С этим разобрались. Теперь к возрастанию. Я не знаю, в каком Вы классе, постараюсь объяснить доступно. Чтобы определить возрастание/убывание функции, нужно взять значения 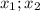 , два произвольных числа, но
, два произвольных числа, но 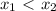 . Пусть мы имеем функцию
. Пусть мы имеем функцию  , тогда вычисляем значения функции в этих двух точках, имеем
, тогда вычисляем значения функции в этих двух точках, имеем 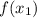 и
и 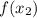 , так вот, если
, так вот, если  , тогда функция возрастающая, если же
, тогда функция возрастающая, если же 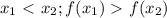 , то она убывающая, но только ПРИ УСЛОВИИ, что она монотонна на всей области определения (т.е. ТОЛЬКО возрастает или ТОЛЬКО убывает), в противном случае мы говорим о ПРОМЕЖУТКАХ возрастания и убывания. 1)
, то она убывающая, но только ПРИ УСЛОВИИ, что она монотонна на всей области определения (т.е. ТОЛЬКО возрастает или ТОЛЬКО убывает), в противном случае мы говорим о ПРОМЕЖУТКАХ возрастания и убывания. 1)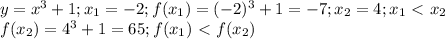 , т.е. функция возрастающая. А вот задание с
, т.е. функция возрастающая. А вот задание с 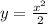 не совсем корректно, так как эта функция возрастает только при x>0, при x<0 она убывает, x=0 - Точка экстремума. Если уж брать математический анализ, то легко взять производную и исследовать функцию на "скорость изменения" (алгебраический смысл производной)
не совсем корректно, так как эта функция возрастает только при x>0, при x<0 она убывает, x=0 - Точка экстремума. Если уж брать математический анализ, то легко взять производную и исследовать функцию на "скорость изменения" (алгебраический смысл производной) 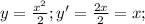 . Если производная в некоторой точке отрицательная, то функция убывает, если производная положительная, то функция возрастает, если производная равна 0, то это точка экстремума. Очевидно, что при x<0 функция убывает, при x>0 возрастает. Если же доказывать возрастание на промежутке x>0, тогда действуем, как и в первом случае (только не берем значения из ненужного нам промежутка):
. Если производная в некоторой точке отрицательная, то функция убывает, если производная положительная, то функция возрастает, если производная равна 0, то это точка экстремума. Очевидно, что при x<0 функция убывает, при x>0 возрастает. Если же доказывать возрастание на промежутке x>0, тогда действуем, как и в первом случае (только не берем значения из ненужного нам промежутка): 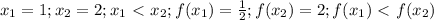 , функция возрастает, что и требовалось доказать.
, функция возрастает, что и требовалось доказать.
1) - x2 - 6x + 27 = 0
x2+6x-27=0
D=36+108=144
x1=(-6+12)/2=3
x2=(-6-12)/2=-9
2) - x2 - 97x - 630 = 0;
x2+97x+630=0
D=97^2-4*630=6889
x1=(-97+83)/2=-7
x2=(-97-83)/2=-90
3) x2 + 12x + 36 = 0
D=12^2-4*36=0
x=-12/2=-6
4) x2 - 3x + 17 = 0;
D=3^2 -4*17=-59
x1=(3+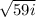 )/2=
)/2=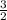 +
+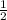
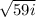
x2=(3-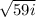 )/2=
)/2=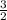 -
-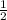
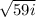
5) x2 - 36x + 324 = 0;
D=(-36)2 - 4·1·324=0
x=36/2=18
6) x2 - 58x + 832 = 0
D=(-58)2 - 4·1·832=36
x1=(58+6)2=32
x2=(58-6)/2=26
7) x2 - 16x - 17 = 0;
D=(-16)2 - 4·1·(-17)=324
x1=(16+18)/2=17
x2=(16-18)/2=-1
8) x2 + 15x + 56 = 0
D=152 - 4·1·56=1
x1=(-15+1)/2=-7
x2=(-15-1)/2=-8