a)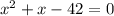 
Ищем дискриминант:
D=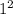
-4*1*(-42)=1-4*(-42)=1-(-4*42)=1-(-168)=1+168=169;
Дискриминант больше 0, уравнение имеет 2 корня: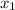
=
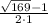=(13-1)/2=12/2=6;
= 
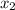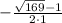=(13-1)/2=12/2=6 =(-13-1)/2=-14/2=-7.
б)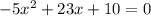 
Ищем дискриминант:
D=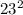
-4*(-5)*10=529-4*(-5)*10=529-(-4*5)*10=529-(-20)*10=529-(-20*10)=529-(-200)=529+200=729;
Дискриминант больше 0, уравнение имеет 2 корня: =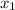 
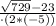=(27-23)/(2*(-5))=4/(2*(-5))=4/(-2*5)=4/(-10)=-4/10=-0.4;
= 
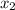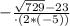=-50/(2*(-5))=-50/(-2*5)=-50/(-10)=-(-50/10)=-(-5)=5.
в)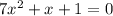 
Ищем дискриминант:
D=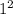-4*7*1=1-4*7=1-28=-27;
Дискриминант меньше 0, уравнение не имеет корней.
г)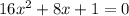 
Ищем дискриминант:
D=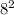 
-4*16*1=64-4*16=64-64=0;
Дискриминант равен 0, уравнение имеет 1 корень:
X=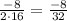
=-0.25
Объяснение:
Принимаем всю работу за единицу (1). ⇒
Скорость выполнения работы одним мастером равна 1/12.
Скорость выполнения работы тремя мастерами равна 3/12=1/4.
Скорость выполнения работы одним учеником равна 1/30.
Скорость выполнения работы учеников впятером равна 5/30=1/6. ⇒
Скорость выполнения работы, когда работают 3 мастера и 5 учеников
одновременно равна:
Таким образом, 3 мастера и 5 учеников работая вместе, выполнят работу за: 1:(5/12)=12/5=2,4 (дня).
ответ: 3 мастера и 5 учеников работая вместе,
выполнят работу за 2,4 дня.