Двузначное число, где а десятков и b единиц представим в виде 10a+b (это разложение числа по разрядам). Далее записываем условие задачи: 1) первое предложение
(10a+b):(a+b)=7(ост.3)
10a+b=7(a+b)+3
10a+b=7a+7b+3
3a-6b=3
a-2b=1 - это первое уравнение системы.
2) читаем второе предложение задачи
При перестановке цифр данного двузначного числа получим число 10b+a. Известно, что оно на 36 меньше, чем число 10a+b. Запишем это: 10a+b-36=10b+a
9a-9b=36 |:9
a-b=4 - это второе уравнение системы
Решаем систему:
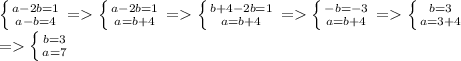
Итак, искомое двузначное число равно 73.
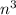 , по условию
, по условию 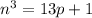 . Перенесём единицу в левую часть и разложим разность кубов на множители:
. Перенесём единицу в левую часть и разложим разность кубов на множители:
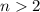 , тогда обе скобки-сомножителя - натуральные числа, большие 1. С другой стороны, произведение
, тогда обе скобки-сомножителя - натуральные числа, большие 1. С другой стороны, произведение 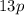 представляется в виде двух натуральных сомножителей, больших единицы, единственным (с точностью до перестановок
представляется в виде двух натуральных сомножителей, больших единицы, единственным (с точностью до перестановок 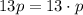 . Поэтому
. Поэтому  ,
,  равны либо
равны либо 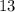 и
и 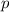 , либо
, либо 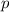 и
и 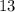 .
.
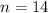 , тогда после подстановки во второе уравнение находим
, тогда после подстановки во второе уравнение находим 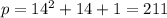 .
.  - действительно простое число, так что
- действительно простое число, так что 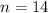 нас устраивает.
нас устраивает.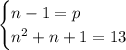
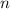 квадратное, а не линейное, как в первом случае. Упростив, получаем уравнение
квадратное, а не линейное, как в первом случае. Упростив, получаем уравнение 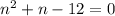 , у которого только один натуральный корень
, у которого только один натуральный корень 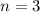 .
. - простое число, так что и тут нас всё устраивает.
- простое число, так что и тут нас всё устраивает. ,
, 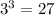
-16
Объяснение:
по теореме Виета получим;
x1+x2=-16