x= - 11 точка локального минимума функции
Объяснение:
Дана функция
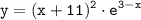
1) Вычислим производную от функции:
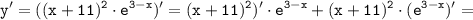
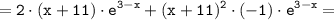
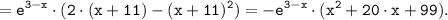
2) Находим критические точки:
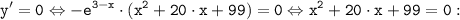
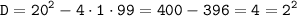
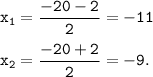
3) Определим промежутки возрастания и убывания функции. Для этого представим производную от функции в следующем виде и применим метод интервалов:
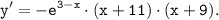
Точки -11 и -9 делят ось Ох на 3 интервала: (-∞; -11), (-11; -9) и (-9; +∞).
а) Пусть x= -12∈(-∞; -11):
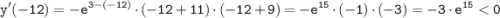
Значит, на интервале (-∞; -11) функция убывает.
б) Пусть x= -10∈(-11; -9):
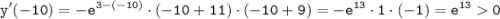
Значит, на интервале (-11; -9) функция возрастает.
в) Пусть x= 0∈(-9; +∞):
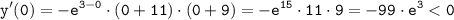
Значит, на интервале (-9; +∞) функция убывает.
4) Определим экстремумы функции:
Функция убывает на интервале (-∞; -11) и возрастает на интервале (-11; -9), то x= - 11 точка локального минимума функции.
Функция возрастает на интервале (-11; -9) и убывает на интервале (-9; +∞), то x= - 9 точка локального максимума функции.
Начало координат - это точка (0;0), поэтому подставляя ее в уравнение прямой, получим с+2=0, откуда с=-2
ответ с=-2