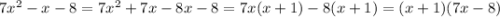
7x²-x-8=0
Сначала решим уравнение через дискриминант.
D=b²-4ac
В данном уравнении: a=7; b=-1; c=-8. Подставляем.
D=(-1)²-4*7*(-8)=1+224=225=15²
Найдём корни по формуле
x=(-b±√D):2a=(-(-1)±15):2*7=(1±15):14
Получаем
x₁=(1-15):14=-14:14=-1
x₂=(1+15):14=16/14=8/7=1 1/7
Есть такая формула для разложения квадратного трёхчлена на множители: ax²+bx+c=a(x-x₁)(x-x₂)
Нам известны корни, подставим их, а также значение A.
7(x+1)(x-1 1/7)
Внесём 7 во вторую скобку, чтобы избавиться от дроби.
7(x+1)(x-8/7)=(x+1)(7x-8)
ответ: 7x²-x-8=(x+1)(7x-8)
Первая производная
f'(x) = 4·(x-5)^3·(x+2)^3+3·(x-5)^2·(x+2)^4
или
f'(x)=7·(x-5)^2·(x-2)·(x+2)^3
Находим нули функции. Для этого приравниваем производную к нулю
(x-5)^2·(x-2)·(x+2)^3 = 0
Откуда
x1 = 5
x2 = -2
x3 = 2
(-∞ ;-2),f'(x) > 0-функция возрастает
(-2; 2),f'(x) < 0-функция убывает
(2; 5),f'(x) > 0-функция возрастает
(5; +∞),f'(x) > 0-функция возрастает
В окрестности точки x = -2 производная функции меняет знак с (+) на (-). Следовательно, точка x = -2 - точка максимума. В окрестности точки x = 2 производная функции меняет знак с (-) на (+). Следовательно, точка x = 2 - точка минимума.