
2. первый член 12, знаменатель 6/12=1/2,
Энный член геометрической прогрессии ищем по формуле bn=b₁*qⁿ⁻¹
b₇=b₁*q⁷⁻¹=b₁*q⁶;
b₇=12*(1/2)⁶=12/64=3/16;
2. b₈=b₁*q⁷=14;
b₁₀=b₁*q⁹=126; разделим b₁₀/b₈=q²=9; q=±3; b₁=14/(±3)⁷=±14/3⁷, используем характеристическое свойство геометрической прогрессии, найдем b₉²=b₈*b₁₀,
b₉²=b₈*b₁₀=126*14;
значит, b₉=±14*3=±42
S₇=b₁*(q⁷-1)/(q-1)
если q=3, S₇=(14/3⁷)*(3⁷-1)/(3-1)=14*2186*/(2*2187)=7*2186*/2187=15302/2187
6 2180/2187
если q=-3, то S₇=
(-14/3⁷)*((-3)⁷-1)/(-3-1)=-14*2188*/(4*2187)=-7*2188*/(2*2187)=-1094*7/2187=
-7658/2187=-3 1097/2187
4. 4.(5)=4+05555=4+0.5+0.05+0.005+...
q=0.05/0.5=0.1
s=0.5/(1-0.1)=5/9
4.(5)=4+(5/9)=4 5/9
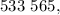 которая должна выражать дату (в каком-то неизвестном представлении).
которая должна выражать дату (в каком-то неизвестном представлении).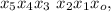


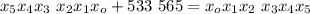 ;
;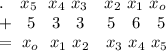

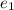 – возможная добавочная единица, уходящая из первого
– возможная добавочная единица, уходящая из первого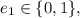
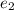 – возможная добавочная единица, уходящая из второго
– возможная добавочная единица, уходящая из второго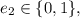
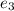 – возможная добавочная единица,
– возможная добавочная единица,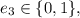
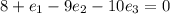 ;
;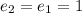 и при
и при  ;
;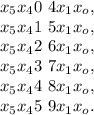
 поскольку
поскольку 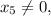 так как с этой цифры начинается разностное число.
так как с этой цифры начинается разностное число. поскольку в первом разряде уже есть шестёрка и добавочная единица, получаемая из нулевого разряда.
поскольку в первом разряде уже есть шестёрка и добавочная единица, получаемая из нулевого разряда.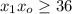 .
.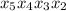 .
.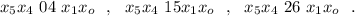
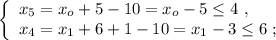

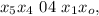
 может играть роль апреля.
может играть роль апреля.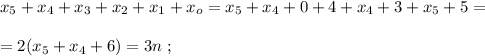
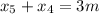 ;
;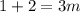 ;
;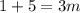 ;
;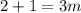 ;
; ;
;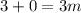 ;
;
 – дата 12/04/56 г.
– дата 12/04/56 г. – дата 15/04/86 г.
– дата 15/04/86 г.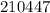 – дата 21/04/47 г.
– дата 21/04/47 г.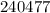 – дата 24/04/77 г.
– дата 24/04/77 г.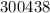 – дата 24/04/38 г.
– дата 24/04/38 г.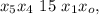
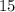 может играть только роль числа месяца (дня).
может играть только роль числа месяца (дня).
 ;
;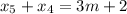 ;
;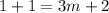 ;
;
 – дата 11/15/46 г.
– дата 11/15/46 г.

В решении.
Объяснение:
1)Решить неравенство:
(х-4)(х+5)<=0
Раскрыть скобки и решить как квадратное уравнение:
х²+5х-4х-20=0
х²+х-20=0, квадратное уравнение, ищем корни:
D=b²-4ac = 1+80=81 √D=9
х₁=(-b-√D)/2a
х₁=(-1-9)/2
х₁= -10/2
х₁= -5
х₂=(-b+√D)/2a
х₂=(-1+9)/2
х₂=8/2
х₂=4
Теперь начертим СХЕМУ параболы (ничего вычислять не нужно), которую выражает данное уравнение, ветви направлены вверх, парабола пересекает ось Ох при х= -5 и х=4, отмечаем эти точки схематично, смотрим на график.
По графику ясно видно, что у<=0 при х от -5 до 4, то есть, решения неравенства находятся в интервале х∈ [-5, 4], причём значения х= -5 и х=4 входят в решения неравенства.
Неравенство нестрогое, скобки квадратные.
2)х²-х-56>0
Схема решения та же.
Находим корни уравнения:
х²-х-56=0
D=b²-4ac = 1+224=225 √D= 15
х₁=(-b-√D)/2a
х₁=(1-15)/2
х₁= -14/2
х₁= -7
х₂=(-b+√D)/2a
х₂=(1+15)/2
х₂=16/2
х₂=8
Также чертим СХЕМУ параболы (ничего вычислять не нужно), которую выражает данное уравнение, ветви направлены вверх, парабола пересекает ось Ох при х= -7 и х=8, отмечаем эти точки схематично, смотрим на график.
По графику ясно видно, что у>0 (как в неравенстве), слева и справа от значений х, то есть, решения неравенства в интервалах
х∈ (-∞, -7)∪(8, +∞).
Неравенство строгое, скобки круглые.
3)Решить систему неравенств:
х²-9<=0
2x-5<0
Первое неравенство решим как квадратное уравнение:
х²=9
х₁,₂= ±√9
х₁,₂= ±3
Снова чертим СХЕМУ параболы, которую выражает данное уравнение, ветви направлены вверх, парабола пересекает ось Ох при х= -3 и х=3, отмечаем эти точки схематично, смотрим на график.
По графику видно, что у<=0 при х от -3 до 3, включая эти значения.
Решение неравенства х∈ [-3, 3].
Неравенство нестрогое, скобки квадратные.
Второе неравенство:
2x-5<0
2x<5
x<2,5
Решение неравенства х∈ (-∞, 2,5)
Неравенство строгое, скобки круглые.
Теперь нужно на числовой оси отметить интервалы решений двух неравенств и найти пересечение решений, то есть, такое решение, которое подходит двум неравенствам.
Чертим числовую ось, отмечаем значения -3, 2,5, 3.
Штриховка по первому неравенству от -3 вправо до 3, от 3 влево до -3.
По второму неравенству штриховка от 2,5 влево до - бесконечности.
Пересечение х∈ [-3, 2,5), это и есть решение системы неравенств.
4)Найти наибольшее целое число из решений неравенства:
(х+5)(х-6)² <0
Первое неравенство:
х+5<0
x< -5
Решение неравенства х∈ (-∞, -5);
Во втором неравенстве свёрнут квадрат разности, развернуть, приравнять к нулю и решить как квадратное уравнение:
х²-12х+36=0
D=b²-4ac = 144-144=0 √D= 0
х₁=(-b-√D)/2a
х₁=(12-0)/2
х₁=6
х₂=(-b+√D)/2a
х₂=(12+0)/2
х₂=6
В уравнении один корень, значит, парабола не пересекает ось Ох, а как бы "стоит " на оси Ох, а х=6 это абсцисса (значение х) вершины параболы.
То есть, вся парабола находится выше оси Ох, и не существует значений х, при котором у<0 (как в неравенстве).
Значит, решением данного неравенства будет интервал х∈ (-∞, -5).
Неравенство строгое, х= -5 не входит в число решений, значит, наибольшим целым числом из решений неравенства будет х= -4.