Будем считать, что площадь равна 150 кв.ед.
Пусть один катет равен x, второй x + a, гипотенуза x + 2a.
При двух неизвестных надо составить 2 уравнения.
Первое по Пифагору.
x² + (x + a)² = (x + 2a)².
x² + x² + 2ax + a² = x² + 4ax + 4a².
x² - 2ax - 3a² = 0. D = 4a² - 4*1*3a² = 16a². √D = 4a.
x₁ = (2a - 4a)/2 = -a (отрицательное значение не принимаем).
x₂ = (2a + 4a)/2 = 3a.
Второе по площади: (1/2)*x*(x + a) = 150.
x² + ax = 300. Вместо х подставим 3a.
9a² + 3a² = 300.
12a² = 300, a² = 300/12 = 25, a = √25 = 5.
Отсюда находим стороны треугольника.
х = 3а = 3*5 = 15.
х + а = 15 + 5 = 20. Это катеты.
Гипотенуза равна 15 + 2*5 = 25.
ответ: 43
Объяснение:
Пусть одно из чисел равно
, тогда второе 
.
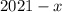Пусть:
Тогда:
Где
и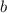 
взаимнопростые натуральные числа. Для определенности будем считать, что 
.
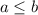Заметим, что числа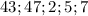
простые. Из второго уравнения очевидно, что 
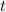не делится на 
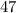, то есть 
.
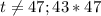Предположим теперь, что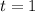
, тогда 
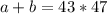, но тогда, поскольку сумма двух чисел делится на 
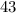, то либо каждое из них делится на 
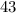, либо не одно из них не делится на 
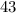. Если каждое из них делится на 
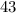, то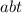 
делится на 
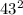, но правая часть второго равенства делится только на первую степень числа 
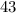. Если же оба из них не делятся на 
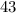, то с учетом того, что 
, 
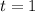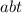не делится на 
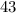. То есть мы пришли к противоречию.
Как видим, остается единственный вариант: