Объяснение:
так, рассмотрим этот пример:
Пример 3, упростить выражение:
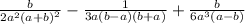
здесь, автор пытался донести, что нам нужно домножить на определенные числа, дабы получить общий знаменатель 6а³(а-b)(a+b)²
При этом, он имел ввиду, что умножение на второй знаменатель можно произвести по разному:
1) если использовать общий множитель
6а³(b-a)(a+b)² , то домножить нужно на 2а²(а+b), и это действительно не принципиально, но тогда третий множитель будет "страдать" - нужно будет домножить его уже со знаком "-": -(a+b)², чтобы при умножении, как вы и сказали: (а-b) = -(b-a) и при умножении двух минусов, мы получаем знак "+"
, так и наоборот для второго случая:
2)если использовать общий множитель
6а³(а-b)(a+b)² , то домножить второй знаменатель нужно на -2а²(а+b)!
А третий на (a+b)², с плюсовым перед стоящим знаком.
И не забываем так же про первый знаменатель :)
Тут всё дело в том, какой общий множитель вы захотите использовать.
Надеюсь, понятно объяснил.
а) 64a² - x² = (8a – x) * (8a + x);
б) x5 – 2x4 + x³ = x³ * (x² - 2x + 1) = x³ * (x – 1)²;
в) 1 – 64z³ = (1 – 4z) * (1 + 4z + 16z²);
г) 36x² - (1 – x)² = (6x – (1 – x)) * (6x + (1 – x)) = (7x – 1) * (5x + 1).
88 + 87 – 86.
Выносим за скобки общий множитель 86 и получаем:
86 * (8² + 8 – 1) = 86 * (64 + 8 – 1) = 86 * 71.
Один из множителей 71, значит, исходное выражение делится на 71. Что и требовалось доказать.
Уравнение.
(x + 1) * (x² - x + 1) = x³ - 2x
x³ - x² + x + x² - x + 1 – x³ + 2x = 0
2x + 1 = 0
2x = -1
x = -0,5.
ответ: х = -0,5.