Раскрываем знак модуля:
Если cosx >0, то |cosx|=cosx
уравнение принимает вид:
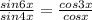
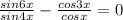
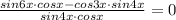
По формуле произведения синуса на косинус:
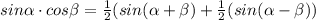
тогда
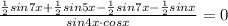
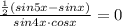
По формуле разности синусов:
⇒ 
⇒ 
⇒ 
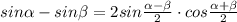
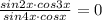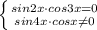
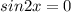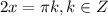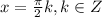
или
⇒ 
⇒ 
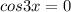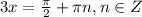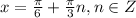
и
⇒ 
⇒ 
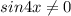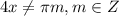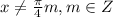
и
⇒ 
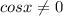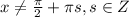
О т в е т первого случая c учетом cosx >0:
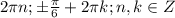( см. рис.1)
Если cosx <0, то |cosx|= - cosx
уравнение принимает вид:
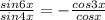
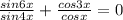
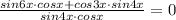
По формуле синуса двойного угла
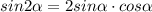
тогда
⇒ 
⇒ 
⇒ 
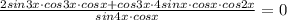
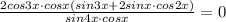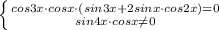
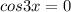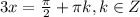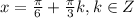
или
⇒ 
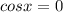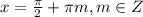
или
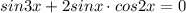
так как
⇒ 
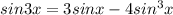
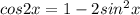
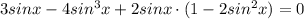
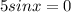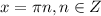
и
⇒ 
⇒ 
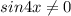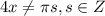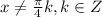
и
⇒ 
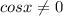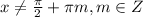
О т в е т второго случая c учетом cosx <0
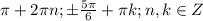( см. рис.2)
О т в е т. Объединяем ответы первого и второго случаев:
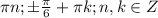
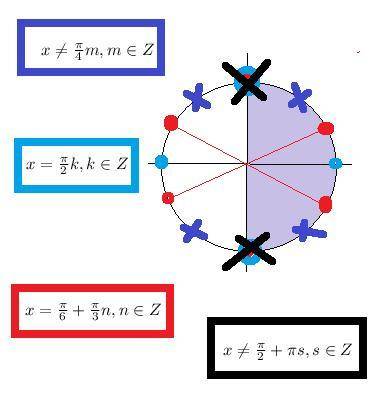
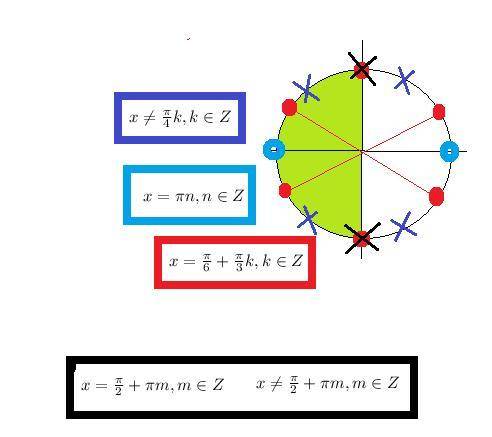
x²-3x=t
t(t+2)-24=0
t²+2t-24=0
D=4+4*24=100=10²
t=(-2+10)/2=4 t=(-2-10)/2=-6
x²-3x=4 x²-3x=-6
x²-3x-4=0 x²-3x+6=0
D=9+16=25 D=9-4*6<0
x=(3+5)/2=4 x=(3-5)/2=-1 x∈∅
ответ: x=4; x=-1