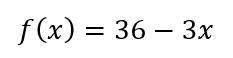
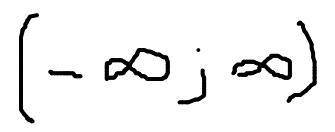
1.
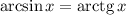
ОДЗ: арксинус определен при ![x\in[-1;\ 1]](/tpl/images/1421/5878/61ea0.png)
Найдем синус левой и правой части:
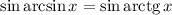
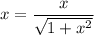
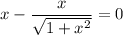
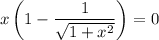
Уравнение распадается на два. Для первого уравнения получим:
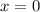
Решаем второе уравнение:
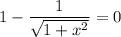
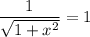
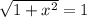
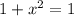
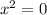
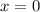
Таким образом, уравнение имеет единственный корень 0.
ответ: 0
2.
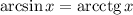
ОДЗ: арксинус определен при
Найдем синус левой и правой части:
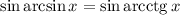
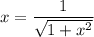
Так как в правой части стоит положительная величина, то и левая часть должна быть положительной, то есть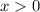 
.
Возведем в квадрат обе части:
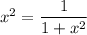
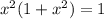
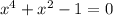
Решим биквадратное уравнение:
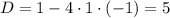
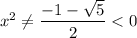
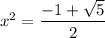
Находим х:
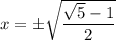
Однако, так как было выявлено ограничение 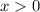, то отрицательный корень не попадает в ответ.
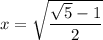
Оценив значение полученного корня, мы понимаем, что он удовлетворяет исходной ОДЗ:
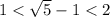
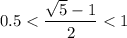
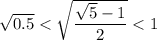
ответ: 
ну неравенств очень много не скажешь что у низ есть какой та определенный алгоритм
Например линейные
2x<5
x<5/2
квадратичные
x^2+2x<0
x(x+2)<0
x<0
x<-2
то есть твоя цель это найти при каких отрезков , то есть значений которых ты найдешь будут являться решениями!
Парабола y=x^2 функцией графика являеться парабола
парабола нужна Допустим в прикладной сфере математики на наибольшее значений нахождение очень полезна то есть ты как бы решаешь какую ту задачу сводишь ее к квадратному, если она сводиться конечно, находишь наибольшее значение
так как она находиться в самом начале параболы а формула известна Ymax=-b/2a
Объяснение:
Функция - линейная, значит обрасть определения ф-ции (-беск;+беск)