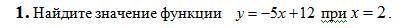
1) sin(π/3 + α) + sin(π/3 - α) = 2 sin (π/3) * cos α = V3 * cos α.
2) sin²(π/4 + α) - sin²(π/4 - α) = (sin(π/4 + α) - sin(π/4 - α)) * ( sin(π/4 + α) + sin(π/4 - α)) =
= (sin π/4 * cos α + cos π/4 *sin α - ( sin π/4 * cos α - cos π/4 *sin α)) *
* (sin π/4 * cos α + cos π/4 *sin α + ( sin π/4 * cos α - cos π/4 *sin α)) =
= ((V2 / 2) * (cos α + sin α) - (V2 / 2) * (cos α - sin α)) *
* ((V2 / 2) * (cos α + sin α)+ (V2 / 2) * (cos α - sin α)) =
= (V2 / 2) * (cos α + sin α - cos α + sin α) * (V2 / 2) * (cos α + sin α + cos α - sin α) =
= 1 / 2 * 2 sin α * cos α = sin α * cos α.
3) cos(π/4 - β) - cos(π/4 + β) = 2 cos (π/4) * cos β = V2 cos β.
4) cos²(α - π/4) - cos²(α + π/4) - аналогично п. 2.
lg(х³-5х²+3х+21) = lg(х³-6х²+4х+27)
Основания у логарифмов равны, поэтому приравняем подлогарифмические выражения.
х³-5х²+3х+21 = х³-6х²+4х+27
х³-5х²+3х+21-х³+6х²-4х-27 = 0
х²-х-6 = 0
По теореме Виета:
х₁*х₂ = -6
х₁+х₂ = 1
х₁ = 3, х₂ = -2
Проверка:
х = -2 подставляем в исходное уравнение.
lg((-2)³-5*(-2)²+3*(-2)+21) = lg((-2)³-6*(-2)²+4*(-2)+27)
lg(-8-20-6+21) = lg(-8-24-8+27)
lg(-13) = lg(-13)
Число, стоящее под знаком логарифма не может быть отрицательным (по определению логарифма). Поэтому число (-2) не является корнем уравнения.
х = 3 подставляем в исходное уравнение.
lg(3³-5*3²+3*3+21) = lg(3³-6*3²+4*3+27)
lg(27-45+9+21) = lg(27-54+12+27)
lg(12) = lg(12)
Равенство верно, число, стоящее под знаком логарифма больше нуля, значит 3 является корнем уравнения.
ответ: х = 3.
y=2
Объяснение:
В формулу вставляем 2
Получается
y=-5*2+12
y=(-10)+12
y=2