Множество M={ 1 ,2 ,3 ,4 ,5 }
Всех двухэлементных подмножеств пятиэлементного множества М будет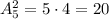 
штук, если учитывать порядок следования элементов . Это такие элементы: 12, 13, 14, 15, 21 , 23, 24, 25, 31, 32, 34, 35, 41, 42, 43, 45, 51, 52, 53, 54 . Здесь элементы 12 и 21 , 34 и 43 и т.д. считаются разными ( как числа) .
Всех двухэлементных подмножеств пятиэлементного множества М будет 
штук, если не учитывать порядок следования элементов . Это такие элементы: 12, 13, 14, 15,23, 24, 25, 34, 35, 45 . Здесь элементы 12 и 21 , 34 и 43 и т.д. считаются одинаковыми, то есть учитывается только то, что, например, первый элемент множества содержит 1 и 2 , восьмой элемент множества содержит 3 и 4 , в любом порядке, поэтому записываем либо пару цифр (1,2) , либо пару (2,1) .
(х-1/3)(х-1/5)<=0.
1.Рассмотрим функцию f(x)= (х-1/3)(х-1/5)
Находим область определения 2.D(f)= (-бесконечность;+бесконечность)
найдем нули функции,т.е. пересечение с осью х. 3.f(x)=0
(х-1/3)(х-1/5)=0
х=1/3
x=1/5
4. Определим знак f(x) на каждом из полученных промежутков на которые область определения разбивается нулями функции.
+ _ _ _ +
..> точки закрашенные,т.к. знак строго меньше или равно
1/3 1/5
(Мы подставляем в исходное уравнение любое число вместо Х,кроме 1/3 и 1/5,в каждом промежутке
т.е. сначала берем любое число от - бесконечности до одной третьей и ставим в уравнение, потом также берем любое число от 1/3 до 1/5 и от 1.5 до бесконечности.
допустим в промежутке от - беск до 1.3 берем число 0,тогда (0-1/3)(0-1/5)
в первой скобке минус,во второй минус, минус на минус будет +. значит знак интервала будет сверху плюс и значит функция f(x) >0.
если х принадлежит (- бесконечность,1/3),то f(x) > 0.
если х прнадлежит (1/3;1/5),то f(x) <0
если x прин-т (1/5;+ бесконечность),то f (x) >0
ответ [1/3; 1/5] скобки квадратные
ответ :12.600
удачи!