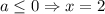1-й случай. x=2 - обращает дробь в ноль. Поэтому x=2 является решением при любом a, за исключением случая, когда поскольку в этом случае знаменатель обращается в ноль.
2-й случай. этот множитель можно отбросить. Получаем
Если числитель отрицателен, знаменатель положителен, поэтому дробь отрицательна, и решений нет.
Если числитель отрицателен, поэтому для положительности дроби нужно, чтобы знаменатель был отрицателен, .
Если a=4, дробь равна нулю; x - любой (естественно, за исключением x=2 - об этом мы говорили раньше).
Если a>4, числитель положителен, поэтому для положительности дроби нужно, чтобы знаменатель был положителен,
2⁵=32 (последняя цифра 2) 2⁶=64 (последняя цифра 4) 2⁷=128 (последняя цифра 8) 2⁸=256 (последняя цифра 6) и т.д. Наблюдаем закономерность - повторение последних цифр степеней числа 2 - это 2,4,8,6
20:4=5 (делится без остатка), значит, последняя цифра числа 2²⁰ равна 6 Т.к. последняя цифра числа 2⁴ также равна 6, получаем, что последняя цифра разности 2²⁰-2⁴ равна 0 (6-6=0). Следовательно, последняя цифра разности 16⁵-2⁴ равна 0. ответ: 0
1-й случай. x=2 - обращает дробь в ноль. Поэтому x=2 является решением при любом a, за исключением случая, когда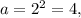 поскольку в этом случае знаменатель обращается в ноль.
поскольку в этом случае знаменатель обращается в ноль.
2-й случай.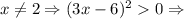 этот множитель можно отбросить. Получаем
этот множитель можно отбросить. Получаем
Если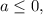 числитель отрицателен, знаменатель положителен, поэтому дробь отрицательна, и решений нет.
числитель отрицателен, знаменатель положителен, поэтому дробь отрицательна, и решений нет.
Если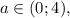 числитель отрицателен, поэтому для положительности дроби нужно, чтобы знаменатель был отрицателен,
числитель отрицателен, поэтому для положительности дроби нужно, чтобы знаменатель был отрицателен, 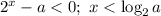 .
.
Если a=4, дробь равна нулю; x - любой (естественно, за исключением x=2 - об этом мы говорили раньше).
Если a>4, числитель положителен, поэтому для положительности дроби нужно, чтобы знаменатель был положителен,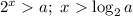
ответ: