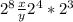
1.a)При возведении степени в степень показатели степеней перемножаются:
(a³)⁴=a¹² (t²)⁵=t¹⁰ (n⁶)⁸=n⁴⁸ (u⁵)⁷=u³⁵ (u⁹)³=u²⁷ (k¹¹)⁴=k⁴⁴
b)Когда двойные скобки, сначала возвести в степень первую скобку, потом вторую:
6(h⁷)⁴=6h²⁸ -2(y⁵)⁶= -2y³⁰ -(d³)⁵= -d¹⁵ ((-2)⁴)²=16²=256
((-3)²)²=9²=81 ((-5)²)²=25²=625
6. При возведении в степень произведения чисел каждый множитель возводится в степень отдельно.
При возведении в степень дроби числитель и знаменатель возводятся в одну и ту же степень:
(ab)⁵=a⁵b⁵
(xyz)⁴=x⁴y⁴z⁴
(-tyu)⁶=t⁶y⁶u⁶
(2n)⁴=2⁴n⁴=16n⁴
(-3xy)³= -3³x³y³= -9x³y³
(0,1cd)²=0,1²c²d²=0,01c²d²
(-1/2sr)⁵= -1⁵/2⁵s⁵r⁵=-1/32s⁵r⁵
(1/3mn)²=1²/3²m²n²=1/9m²n²
Пересечение графика с осью абсцисс (т.е. с горизонтальной) — это корни уравнения ax²+bx+c=0
Корни уравнения в данном случае — это 5 и (-1)
По теореме Виета в уравнении ax²+bx+c=0: с=5*(-1)=-5, -b=5-1=4, т.е. b=-4
Экстремум квадратичной функции — это вершина параболы. Вершина параболы находится по формуле ув.=(4ac-b²)/(4a), где ув. — координата вершины по игрику.
Нам известны yв., в и с. Cоставим уравнение.
-9=(4*a*(-5)-16)/(4a)
…
a=1
ответ: y=x²-4x-5.