График функции y=3/x - гипербола, расположена в первой и третьей четвертях. Точки для построения :
x = 1/2; y = 3/(1/2) = 6; A(1/2; 6)
x = -1/2; y = 3/(-1/2) = -6; A'(-1/2; -6)
x = 1; y = 3/1 = 3; B(1; 3)
x = -1; y = 3/(-1) = -3; B'(-1; -3)
x = 2; y = 3/2 = 1,5; C(2; 1,5)
x = -2; y = 3/(-2) = -1,5; C'(-2; -1,5)
x = 3; y = 3/3 = 1; D(3; 1)
x = -3; y = 3/(-3) = -1; D'(-3; -1)
Область определения функции D(y) = (-∞; 0)∪(0; +∞)
Область значений функции E(y) = (-∞; 0)∪(0; +∞)
Функция убывает на всей области определения D(y) = (-∞; 0)∪(0; +∞)
Промежутки знакопостоянства :
y > 0 при x ∈ (0; +∞)
y < 0 при x ∈ (-∞; 0)
Функция нулей не имеет, пересечений с осью OY тоже.
Функция нечетная : y(-x) = 3/(-x) = -3/x = -y(x)
Функция не периодичная.
Функция имеет две асимптоты :
горизонтальную y=0 и вертикальную x=0
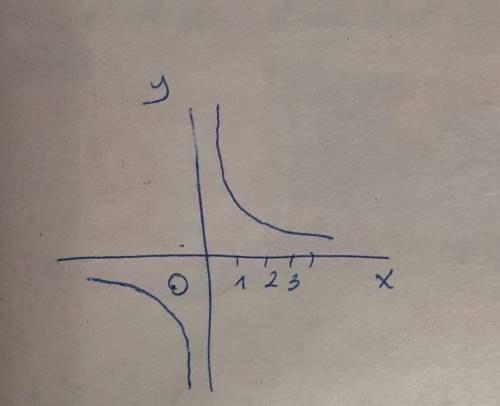
ответ: 4132 .
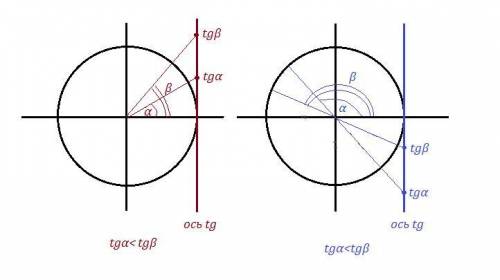
Угловой коэффициент прямой k - это тангенс угла наклона ( tgα ) прямой к положительному направлению оси ОХ.
Все острые углы α имеют положительный tgα>0 , а тупые углы - отрицательный tgα<0 .
Прямые 1 и 4 наклонены под острым углом, значит их угловые коэффициенты положительны ( k₁>0 , k₄>0 ) . А прямые 2 и 3 наклонены под тупым углом к оси ОХ , значит их угловые коэффициенты отрицательны ( k₂<0 , k₃<0 ) .
Все положительные числа больше отрицательных . Теперь сравним между собой k₁ и k₄ , а также k₂ и k₃ .
Чем больше острый угол, тем больше tg этого угла , значит k₄>k₁ .
Чем меньше тупой угол, тем меньше tg этого угла, значит k₃>k₂ .
Окончательно получаем: k₄>k₁>k₃>k₂ .
p = m/n,
n = 6·6 = 36.
Найдем те варианты выпадения костей, при которых сумма очков равна семи: (1;6), (6;1), (2;5), (5;2), (3;4), (4;3).
Теперь из найденных вариантов найдём те, разность выпавших очков на которых равна четырём (вычитаем из большего меньшее). Очевидно, что таких вариантов нет. Тогда m = 0.
p = 0/36 = 0.
ответ. 0.