где S - наращенная сумма (сумма которую получит клиент через n лет), P - сумма вклада, i - процентная ставка(годовых), n - срок.
Клиент А положил в банк 3800 рублей, тогда через год он получит рублей. В тех же условиях через год клиент Б получит рублей, в это же время два года для клиента А, он должен получить рублей. Зная, что клиент А получил на 418 рублей больше клиента Б, составим уравнение:
Решаем как квадратное уравнение относительно (1+i)
i₁ < 0 т.е. оно не удовлетворяет условию;
Т.е. под 10% годовых начислял банк по этим вкладам.
Сначала надо разобраться со знаменателем: log₁/₃log₃9 = log₁/₃2 разберёмся теперь со знаком знаменателя: log₁/₃ 2 = x, ⇒ 2 =(1/3)ˣ, lg2 = x lg(1/3), ⇒ lg2 = x*(lg1 - lg3) ,⇒lg2 = -xlg3,⇒ ⇒x = -lg3/lg2 это число отрицательное. Вывод: в знаменателе стоит отрицательное число, вся данная дробь >0, значит, числитель должен быть отрицательным. log₅(2x -3) < 0 с учётом ОДЗ и с учётом того,что данная логарифмическая функция возрастающая , составим систему неравенств: 2x - 3 > 0 x > 1,5 2x - 3< 1 решаем: x < 2 ответ: х∈(1,5; 2)
Формула сложной процентной ставки: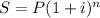
где S - наращенная сумма (сумма которую получит клиент через n лет), P - сумма вклада, i - процентная ставка(годовых), n - срок.
Клиент А положил в банк 3800 рублей, тогда через год он получит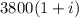
рублей. В тех же условиях через год клиент Б получит 
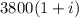рублей, в это же время два года для клиента А, он должен получить 
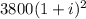рублей. Зная, что клиент А получил на 418 рублей больше клиента Б, составим уравнение:
Решаем как квадратное уравнение относительно (1+i)
i₁ < 0 т.е. оно не удовлетворяет условию;
Т.е. под 10% годовых начислял банк по этим вкладам.
ответ: 10 %.