Объяснение:
у= х-4 искомое уравнение.
Объяснение:
Прямая y=kx+b проходит через точки C (5; 1) и D (1 ;-3). Запишите уравнение это прямой.
Формула, при которой можно построить уравнение прямой по двум точкам:
(х-х₁)/(х₂-х₁)=(у-у₁)/(у₂-у₁)
C (5; 1) и D (1 ;-3)
х₁= 5 у₁=1
х₂= 1 у₂= -3
Подставляем данные в формулу:
(х-5)/(1-5)=(у-1)/(-3)-1)
(х-5)/(-4)=(у-1)/(-4) перемножаем крест-накрест, как в пропорции:
(-4)(х-5)=(-4)(у-1)
-4х+20= -4у+4
4у=4х+4-20
4у=4х-16
4у= 4х-16/4
у= х-4 искомое уравнение
.
Объяснение:
1. Постройте график функции y=2x-1. По графику найдите: а) значения функции при значениях аргумента, равных -2;0;3; б)
значения аргумента, при которых значения функции равны 3;7; в) найдите точку пересечения данной прямой с прямой, заданной уравнением x=4
Функция у = 2х - 1 является линейной функцией, то есть графиком данной функции будет прямая. Для построения прямой достаточно двух точек.
х = 1; у = 2 * 1 - 1 = 1. Точка (1; 1).
х = 5; у = 2 * 5 - 1 = 9. Точка (5; 9).
Чертим координатную плоскость, ставим точки, проводим прямую.
а) Значения функции - это значение у, значение аргумента - это значение х. Находим точки -2, 0 и 3 на оси х, мысленно проводим вертикальную прямую и определяем координату у в точке на прямой.
х = -2; у = -5.
х = 0; у = -1.
х = 3; у = 5.
б) Находим точки 3 и 7 на оси у, мысленно проводим горизонтальную прямую, определяем координату х на прямой.
у = 3; х = 2, точка (3; 2).
у = 7; х = 4.
в) Прямая х = 4 - это вертикальная прямая, пересекающая ось х в точке 4. Чертим данную прямую, определяем координаты точки пересечения. Точка (4; 7)
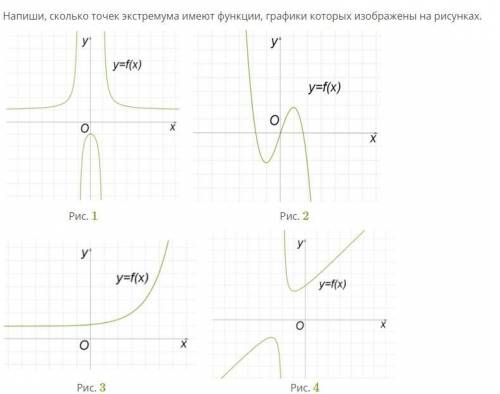
ответ: на рис.1 - 1 точка; на рис.2 - 2 точки; на рис.3 - нет точек; на рис.4 - 2 точки экстремума. ответ:на рис.4 - 2 точки экстремума
Объяснение: Точки экстремума - это точки , где функция меняет свое поведение с возрастания на убывание или наоборот (т. е. выпуклость или вогнутость). При переходе через точку максимума изменяется характер монотонности функции: слева от точки максимума функция возрастает, справа —убывает. При переходе через точку минимума изменяется характер монотонности функции: слева от точки минимума функция убывает, справа —возрастает.