Определить промежутки монотонности функции, не используя производную функции.
y = (x² - x - 20)² - 18
=================================
Область определения функции D (y) = R
y = (x² - x - 20)² - 18
Квадратичная функция в квадратичной функции
y = f(z); z = g(x)
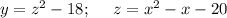
Чтобы найти промежутки монотонности квадратичной функции, нужно найти абсциссу вершины параболы.
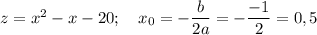 - координата вершины
- координата вершины
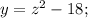 z = 0 - координата вершины параболы
z = 0 - координата вершины параболы

x₁ = -4; x₂ = 5 - координаты вершин параболы
Таким образом, есть три точки, которые определяют промежутки монотонности функции y = (x² - x - 20)² - 18.
x₁ = -4; x₀ = 0,5; x₂ = 5
x ∈ (-∞; -4] - функция убывает : y(-5) > y(-4)
x ∈ [-4; 0,5] - функция возрастает : y(-4) < y(0)
x ∈ [0,5; 5] - функция убывает : y(1) > y(2)
x ∈ [5; +∞) - функция возрастает : y(5) < y(6)
1) отрицательное,т,к при умножение 2-х чисел в разными знаками,прооизведение отрицательное
2) положительное,так как при деление двух чисел с одинаковыми знаками частное положительное
3)отрицательное,приведем показатели степени в общему знаменателю
получим 42 в степени 9/21 53 в степени 14/21
второе число большее,поэтому и знак будет минус
4)отрицательное т,к
1 представим,как 2в степени 0.получим,что второе опять больше первого
5)положительное,так как при сложение 2-х полодительный сумма положительная
1) -4x + 6x = -7 - 3
2x = -10
x = -5
2) -3x -2x = 10 - 5
-5x = 5
x = -1
3) 2x + 5x = 9 - 6
7x = 3
x = 3/7