= (2³ + (2¹¹)³)( 2⁶ - 2³⁶+ 2⁶⁶) =
= (2 + 2¹¹)(2² – 2¹² + 2²²) ( 2⁶ - 2³⁶ + 2⁶⁶) =
= 2(1 + 2¹⁰)(2² – 2¹² + 2²²) ( 2⁶ - 2³⁶ + 2⁶⁶) =
= 2 (1 + 1024)(4 – 2¹² + 2²²) ( 2⁶ - 2³⁶+ 2⁶⁶) =
= 2 ∙ 1025 ∙ (4 – 2¹² + 2²²) ( 2⁶ - 2³⁶+ 2⁶⁶)
Выражение 2⁹ + 2⁹⁹ имеет 4 множителя, один из которых делится на число 41.
1025 : 41 = 25
А если хотя бы один из множителей разделился на 41, то значит и всё выражение 2⁹ + 2⁹⁹ разделится на 41.
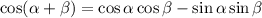
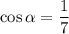- положительное число, значит косинус расположен либо в 1 четверти либо в 4 четверти, то есть, будем рассматривать 2 случая:
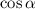в первой четверти, тогда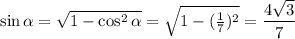
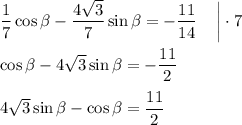
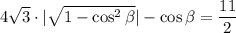
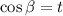
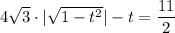
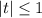мы можем убрать модуль: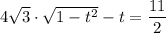
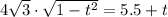
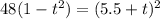
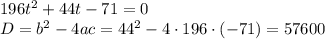
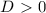, значит квадратное уравнение имеет 2 корня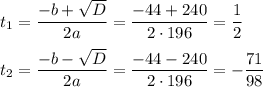
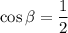- подходит
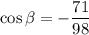- подходит.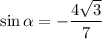
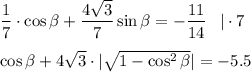
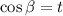
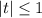уравнение имеет вид: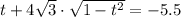 
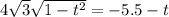
отсюда 
,то в левой части уравнения подкоренное выражение будет иметь всегда отрицательное значение. Значит, уравнение решений не имеет.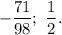
B2c-9c=C*(2b-9)
Объяснение:
B2c-9c=C*(2b-9)