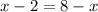
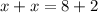
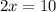
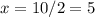
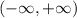, но не принадлежит 
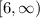, ![(-\infty, 0]](/tpl/images/0408/1975/03e35.png)
, 
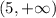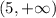.. Тут круглая скобка перед 5 означает, что точка x=5 исключена "вырезана" из интервала, а квадратная означает, что точка включена в интервал. Вот, например x=5 принадлежит интервалу 
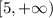. Если обе крайние точки принадлежат интервалу, то насколько мне помнится его называют "отрезок".
1)
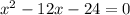
данное уравнение имеет два различных корня.
по теореме Виета:
Т.к. произведение корней отрицательно, то два корня разных знаков: меньший - отрицательный, больший - положительный.
2)
уравнение имеет два различных корня.
по теореме Виета:
Т.к. произведение корней положительно, то имеет два корня одного знака, а т.к. сумма корней положительна, то имеет два положительных корня.
3)
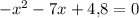
уравнение имеет два различных корня. По т. Виета:
Т.к. произведение корней отрицательно, то имеет два корня различных знаков: меньший - отрицательный, больший - положительный.
4)
уравнение имеет два различных корня. По т. Виета:
Т.к. произведение корней отрицательно, то имеет два корня разных знаков: меньший - отрицательный, больший - положительный.