В решении.
Объяснение:
1.
а) b/√7 * √7/√7 = b√7/7;
б) 5/√x *√x/√x = 5√x/x;
в) 5/3√6 *√6/√6 = 5√6/3*6 = 5√6/18;
г) 12/7√2 *√2/√2 = 12√2/7*2 = 12√2/14 = 6√2/7;
д) 1/√3 * √3/√3 = √3/3;
е) 5/4√5 * √5/√5 = 5√5/4*5 = 5√5/20 = √5/4.
2.
а) 2/(√c+y) * (√c+y)/(√c+y) = 2(√c+y)/(c+y);
б) 6/(√5 + 1) * (√5 - 1)/(√5 - 1) =
в знаменателе развёрнутая разность квадратов, свернуть:
= 6(√5 - 1)/(√5)² - 1² =
= 6(√5 - 1)/(5 - 1) =
= 6(√5 - 1)/4 =
= 3(√5 - 1)/2;
в) с/(√a - √c) * (√a + √c)/(√a + √c) =
в знаменателе развёрнутая разность квадратов, свернуть:
= c(√a + √c)/(√a)² - (√c)² =
= c(√a + √c)/(a - c);
г) k/(x + √k) * (x - √k)/(x - √k) =
в знаменателе развёрнутая разность квадратов, свернуть:
= k(x - √k)/(x² - (√k)²) =
= k(x - √k)/(x² - k);
д) 5/(√13 + √3) * (√13 - √3)/(√13 - √3) =
в знаменателе развёрнутая разность квадратов, свернуть:
= 5(√13 - √3)/(√13)² - (√3)² =
= 5(√13 - √3)/(13 - 3) =
= 5(√13 - √3)/10 =
= (√13 - √3)/2;
е) 6/(5 - 2√6) * (5 + 2√6)/(5 + 2√6) =
в знаменателе развёрнутая разность квадратов, свернуть:
= 6(5 + 2√6)/(5² - (2√6)²) =
= 6(5 + 2√6)/(25 - 4*6) =
= 6(5 + 2√6)/1 =
= 6(5 + 2√6).
ДАЮ 100Б ЗА РЕШЕНИЕ ЗА 30М
ответ у меня есть , но нужно обьяснение
Золотоискатель нашёл кристалл кварца с кусочком чистого золота внутри. Он надеялся хорошо заработать на продаже кристалла и не стал вынимать из него золото. Ювелир взвесил и измерил кристалл. Масса кристалла оказалась равной 100 г, объем 12,5 см3. Ювелир согласился заплатить только за чистое золото. После некоторых расчётов ювелир сказал золотоискателю, что масса чистого золота 64 г. Сколько грамм чистого золота ювелир нечестно присвоил себе, не оплатив золотоискателю? Плотность золота 19,3 г/см3, плотность кварца 2,7 г/см3. ответ выразите в граммах, округлите до целого числа.
Упростите выражение:
Выносим общий множитель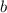 за скобки в числителе первой дроби:
за скобки в числителе первой дроби:
И общий множитель в знаменателе второй дроби:
в знаменателе второй дроби:
Сокращаем в знаменателе первой дроби и
в знаменателе первой дроби и 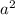 в числителе второй дроби:
в числителе второй дроби:
И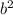 в знаменателе первой дроби и
в знаменателе первой дроби и 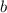 в числителе второй дроби:
в числителе второй дроби:
Раскладываем на множители (по формуле разности квадратов) выражение в числителе первой дроби:
в числителе первой дроби:
Сокращаем первую дробь на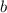 :
:
А вторую дробь на :
:
Сокращаем в числителе первой дроби и в знаменателе второй дроби:
в числителе первой дроби и в знаменателе второй дроби:
Выражение упрощено!