Вариант №1
1. Найдите производнуй функций
y= sin(x^2-〖3x〗^2)
2. Найдите область определения функций
y=lg(x2-5x+6)
3. Определите точки экстремума функций
y= x4-2x2+1
4. Определите наименьшее и наибольшее значение функций
y=x5-5x4+5x3+3 на отрезке [-1; 2]
Вариант №2
1. Найдите интеграл ∫▒〖6x^2 (1-x^3)dx〗
2. Определите плошадь фигуры, ограниченный линиями y=x2, x= -1, x=2 и y=0.
3. Вычислить интеграл ∫_1^2▒dx/x по формуле прямоугольника при n=10 с точностью до 0,01
4. Скорость движения тела изменяется по закону V(t)=3t 2. Найди путь, пройденный телом за 7с. от начало движения
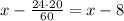км. Скорость по течению равна (24+6=30)км/ч, а против течения - (24-6=18) км/ч. Так как катер дошёл до середины и обратно вернулся, то на весь путь он затратил 
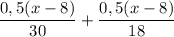что составляет 3 часа - 20 мин = 3 ч - 20/60 ч = 8/3.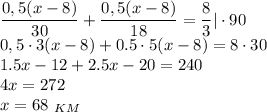
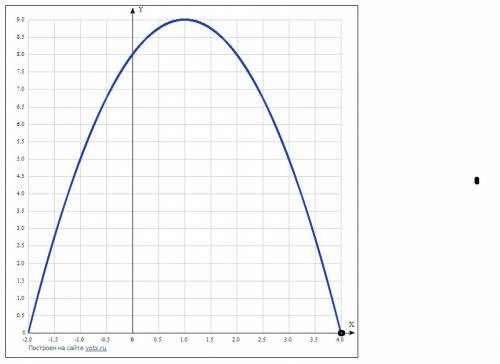
1 вариант. Второй решен в других ваших вопросах. Зачем по сто раз один вопрос задавать?