Для того, чтобы вычислить вероятность, сначала посмотрим на возможные исходы. Бросаем 2 монетки, значит могут быть следующие исходы:
1)на 1 монете выпадет ОРЕЛ, на второй ОРЕЛ
2)на 1 выпадет ОРЕЛ, на второй РЕШКА
3)на 1 выпадет РЕШКА, на второй ОРЕЛ
4)на 1 выпадет РЕШКА, на второй РЕШКА.
Больше исходов быть не может. Вспомнои формулу нахождения вероятности:
P=m/n, где m - благоприятные исходы, n - все исходы.
В нашем случае: Р=1 (потому что в перечисленных вышеискодах один раз выпадает два орла) / 4 (потому что мы посчитали, что исходов в даннной ситуации четыре)=0,25
ответ: 0,25
1) Из первого уравнения y=3x-10, подставим во второе: x^2 - (3x-10)^2=20-x(3x-10)
x^2 -(9x^2 -60x +100) = 20-3x^2 +10x, -8x^2 + 60x - 100 + 3x^2 -10x - 20 = 0,
-5x^2 +50x - 120 = 0, делим на (-5): x^2 -10x + 24 = 0; теорема Виета: x = 4; 6
Теперь найдем у. Если х = 4, то у = 3*4-10= 2; если х=6, то у=3*6-10=8
ответ: { (4; 2) , (6; 8) }
2) b1 + b2 + b3 = 39, b1 + b1*q + b1*q^2 = 39, b1(1 + 4 + 16) = 39, b1*21 = 39,
b1 = 39/21 = 13/7. Тогда b4 = b1*q^3 = (13/7)*64=832/7 = 118 целых 6/7
S4=39 + 118 целых 6/7 = 157 целых 6/7
Продифференцируем первое уравнение:
Подставим в него соотношение для y' из второго уравнения:
Из полученного уравнения отнимем первое уравнение системы, умноженное на 5:
Составим характеристическое уравнение:
Найдем х':
Выразим у из первого уравнения:
Находим у:
Условие для задачи Коши:
От первого уравнения отнимем второе:
Выражаем из первого уравнения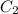 :
:
Частное решение: