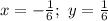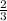 от того, что осталось после первого деня, то после второго дня работы осталась
от того, что осталось после первого деня, то после второго дня работы осталась  от того, что осталось после первого дня работы. По условию, после двух дней работы осталось 2 банки, соответственно
от того, что осталось после первого дня работы. По условию, после двух дней работы осталось 2 банки, соответственно  =2, из чего следует, что во второй день израсходовали 4 банки с краской (так как 2×2=4). По условию сказано, что в первый день израсходовали половину всех банок +1. Значит, 4 банки - это половина всех банок -1. Соответственно, половина - это 4+1=5. В первый день израсходовали 5+1=6 (банок с краской), во второй день израсходовали 4 (банки с краской), а осталось на третий день еще 2 (банки с краской). Суммируем все количество банок: 6+4+2=12.
=2, из чего следует, что во второй день израсходовали 4 банки с краской (так как 2×2=4). По условию сказано, что в первый день израсходовали половину всех банок +1. Значит, 4 банки - это половина всех банок -1. Соответственно, половина - это 4+1=5. В первый день израсходовали 5+1=6 (банок с краской), во второй день израсходовали 4 (банки с краской), а осталось на третий день еще 2 (банки с краской). Суммируем все количество банок: 6+4+2=12.1. -15 ≤ 1-2у ≤ 0
2. 
Объяснение:
1. Т.к. в линейном выражении 1-2у перед у стоит знак "-", то при вычислении пределов возможных значений нужно либо поменять направление знаков больше (меньше) либо поменять местами подставляемые значения 1/2 и 8.
для 1/2 ≤ у: 1-2у ≤ 0
для у ≤ 8: 1-2у ≥ -15
Тогда: -15 ≤ 1-2у ≤ 0
2. Здесь перед у знак "+", но появилась нелинейная зависимость 4/у, поэтому нужно вычислить производную функции (4/у + у) и приравнять её к нулю, чтобы найти ее экстремум.
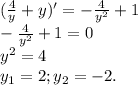
Но так как значение -2 не попадает в наш промежуток по условию, то это значение отбрасываем.
Значит, в точке у=2 имеем экстремум. Определим его значение:
для у=2: 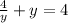 .
.
На остальных участках функция либо возрастает, либо убывает. подставим граничные значения из условия:
для у=1/2 : 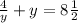
для у=8: 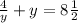 .
.
Т.е. имеем кривую с максимумами 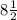 и минимумом 4.
и минимумом 4.
Тогда 
Смысл задачи: найти такие x и y, чтобы это равенство было справедливо при всех допустимых значений a (то есть для всех, кроме -4 и 2).
1-й
2-й
Запишем равенство в виде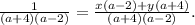
знаменатели в левой и правой части совпадают, поэтому совпадают числители:
x(a-2)+y(a+4)=1.
Дальше у нас есть две возможности рассуждения. При первой подставляем в это равенство a=2, находя при этом y=1/6, а затем подставляем a=-4, находя x=-1/6.
При втором рассуждения запишем равенство в виде
(x+y)a+(-2x+4y)=1. Поскольку это равенство должно быть справедливо при всех значениях a, получаем систему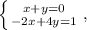 решив которую, получим те же значения x и y.
решив которую, получим те же значения x и y.
ответ: