Объяснение:
Функция задана формулой y = −3x + 1. Определите:
1) значение функции, если значение аргумента равно 4;
2) значение аргумента, при котором значение функции равно −5;
3) проходит ли график функции через точку A (−2; 7).
1)y = −3x + 1
Построить график. График линейной функции, прямая линия. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
Таблица:
х -1 0 1
у 4 1 -2
а)Чтобы найти значение у, нужно известное значение х подставить в уравнение и вычислить у:
х=4
у= -3*4+1= -11 при х=4 у= -11
б)Чтобы найти значение х, нужно известное значение у подставить в уравнение и вычислить х:
у= -5
-5= -3х+1
3х=1+5
3х=6
х=2 у= -5 при х=2
в)Чтобы определить принадлежность точки графику, нужно известные значения х и у (координаты точки) подставить в уравнение, если левая часть будет равна правой, значит, точка принадлежит графику и наоборот.
A (−2; 7)
y = −3x + 1
7= -3*(-2)+1
7=6+1
7=7, проходит.
2)Постройте график функции y = 2x − 5. Пользуясь графиком, найдите:
1) значение функции, если значение аргумента равно 3;
2) значение аргумента, при котором значение функции равно −1.
Построить график. График линейной функции, прямая линия. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
y = 2x − 5
Таблица:
х -1 0 1
у -7 -5 -3
б)согласно графика, при х=3 у=1
согласно графика у= -1 при х=2
3)Не выполняя построения, найдите координаты точек пересечения
графика функции y = −0,6x + 3 с осями координат.
а)График пересекает ось Оу при х=0:
х=0
у= -6*0+3=3
Координаты точки пересечения графиком оси Оу (0; 3)
б)График пересекает ось Ох при у=0.
у=0
0= -0,6х+3
0,6х=3
х=5
Координаты точки пересечения графиком оси Ох (5; 0)
4)При каком значении k график функции y = kx+ 5 проходит через точку D (6; −19)?
Подставляем известные значения х и у (координаты точки D) в уравнение и вычисляем k:
y = kx+ 5
-19=k*6+5
-6k=5+19
-6k=24
k= -4
Какой формулой пользоваться значения не имеет. На фотографиях представлены решения уравнения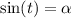 .
.
Если нарисовать числовую окружность, то значение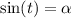 есть координата точки
есть координата точки  по оси
по оси  , ведь для любой точки числовой окружности справедливо, что
, ведь для любой точки числовой окружности справедливо, что 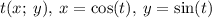 , т.е. точка
, т.е. точка 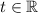 имеет координаты
имеет координаты 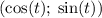 .
.
Если провести прямую, параллельную оси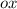 через точку
через точку 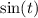 , то она пересечётся с числовой окружностью в каких-то точках.
, то она пересечётся с числовой окружностью в каких-то точках.
Чтобы было понятнее, советую нарисовать окружность радиусом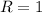 и центром в точке
и центром в точке 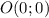 и отмечать всё, о чём я пишу.
и отмечать всё, о чём я пишу.
Теперь рассмотрим эти точки пересечения.
Если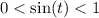 , то пересечения будут в первой и второй четвертях.
, то пересечения будут в первой и второй четвертях.
Если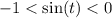 , то пересечения будут в третьей и четвёртой четвертях.
, то пересечения будут в третьей и четвёртой четвертях.
Если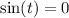 , то пересечений тоже два и это
, то пересечений тоже два и это 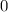 и
и 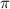 .
.
Если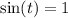 , то пересечение только одно, при чём точка пересечения будет и точкой касания, и равна она
, то пересечение только одно, при чём точка пересечения будет и точкой касания, и равна она 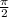 .
.
Если же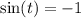 , то пересечение тоже одно, тоже является точкой касания, но значение равно
, то пересечение тоже одно, тоже является точкой касания, но значение равно 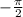 .
.
А теперь вспомним определение арксинуса. Арксинусом числа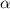 называют такой угол
называют такой угол 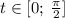 , что
, что 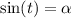 . Главное здесь то, что
. Главное здесь то, что 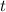 может быть углом только первой четверти.
может быть углом только первой четверти.
Отсюда же следует, что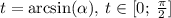 .
.
Это прекрасно работает для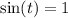 , ведь
, ведь 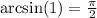 .
.
Но только недавно мы проверили, что у нас может быть и не одно, а два решения. Как поступить в случае, если арксинус работает только для углов первой четверти, а нам нужно, чтобы он работал во второй? ответ прост.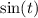 - это число, а
- это число, а 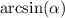 - угол.
- угол.
Пусть прямая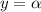 пересекается с окружностью в точках
пересекается с окружностью в точках 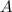 в первой четверти и
в первой четверти и 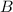 во второй четверти, а точку
во второй четверти, а точку 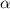 на оси
на оси 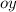 мы обзовём
мы обзовём 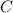 . Рассмотрим треугольники
. Рассмотрим треугольники 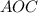 и
и 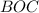 , в них:
, в них:
Треугольники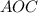 и
и 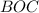 равны по двум катетам. Из этого следует и то, что их соответственные углы равны. Т.е. угол
равны по двум катетам. Из этого следует и то, что их соответственные углы равны. Т.е. угол 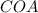 и угол
и угол 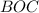 .
.
Но углы мы отсчитываем от точки , обзовём её
, обзовём её 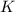 . Тогда угол
. Тогда угол 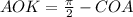 . А это угол
. А это угол 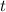 первой четверти.
первой четверти.
А угол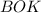 - искомый угол второй четверти.
- искомый угол второй четверти.
Как нам известно, все числа на числовой окружности получаются с поворота на определённый угол, пусть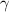 - этот угол. И если мы сделаем полный оборот, то мы хоть и придём в ту же самую точку, но вот число уже будет другое, ведь поворачивались мы на другой угол, равный
- этот угол. И если мы сделаем полный оборот, то мы хоть и придём в ту же самую точку, но вот число уже будет другое, ведь поворачивались мы на другой угол, равный 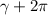 . Таким образом, чтобы описать все числа, находящиеся в точке на окружности с координатами
. Таким образом, чтобы описать все числа, находящиеся в точке на окружности с координатами 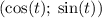 надо добавить
надо добавить 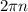 , где
, где 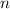 - целое (чтобы получились полные обороты).
- целое (чтобы получились полные обороты).
Вот так и получается первая формула.
Что до второй, то тут всё проще. Выводить её не буду, и так ответ уже километровый. В ней всё работает на чётности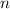 . Если
. Если 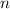 - чётное, то формула трансформируется в
- чётное, то формула трансформируется в 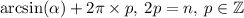 , если нечётное, то в
, если нечётное, то в 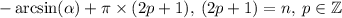 , ну а
, ну а 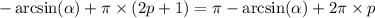 . Т.е. это тоже самое, только записанное в одну строчку. Использовать вторую формулу не советую. Она менее интуитивно понятная. Но если в ней разобраться, то решение уменьшается в размере, это правда.
. Т.е. это тоже самое, только записанное в одну строчку. Использовать вторую формулу не советую. Она менее интуитивно понятная. Но если в ней разобраться, то решение уменьшается в размере, это правда.
Как-то так. Фу-у-у-ух. Много. Очень Много Букв.
P.S. Прости за задержку.