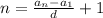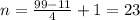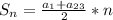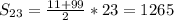Question

Найдите, множество первообразных для функции

Answer 1

$f(x)=\dfrac{2\, dx}{(3x-4)^3}\\\\\\F(x)=\int \dfrac{2\, dx}{(3x-4)^3}=\Big[\; t=3x-4\ ,\ dt=3\, dx\; \Big]=\dfrac{2}{3}\int \dfrac{dt}{t^3}=\dfrac{2}{3}\cdot \dfrac{t^{-2}}{-2}+C=\\\\\\=-\dfrac{1}{3\, t^2}+C=-\dfrac{1}{3\, (3x-4)^2}+C$

Answer 2

если подвести под знак дифференциала (3х-4),то получим dx=d(3x-4)/3

∫2dx/(3x-4)³=(2/3)∫d(3x-4)/(3x-4)³ и, используя инвариантность интеграла, найдем множество первообразных,

∫2dx/(3x-4)³=(2/3)∫d(3x-4)/(3x-4)³=(-(2/3)*(1/2)*/(3x-4)²)+с=

(-1/3)*(1/(3х-4)²)+с