1/2 или 0,5
Объяснение:
![\sqrt{\frac{4}{25} } + \sqrt[3]{\frac{1}{1000} } \\\frac{2}{5} + \frac{1}{10} \\\frac{1}{2}](/tpl/images/1338/0962/7386b.png)
Определим общее число расстановок на пяти позициях 5 шариков:
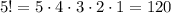
Однако, среди этих расстановок есть недопустимые (то есть те, при которых между зеленым и желтым шариком располагаются два или более шарика). Найдем число недопустимых расстановок.
Найдем число недопустимых размещений зеленого и желтого шарика. Их можно просто перечислить:
1) зеленый на 1-ом месте, желтый на 4-ом месте
2) зеленый на 1-ом месте, желтый на 5-ом месте
3) зеленый на 2-ом месте, желтый на 5-ом месте
4) зеленый на 4-ом месте, желтый на 1-ом месте
5) зеленый на 5-ом месте, желтый на 1-ом месте
6) зеленый на 5-ом месте, желтый на 1-ом месте
В каждом из этих случаев оставшиеся три шарика могут размещаться на свободных местах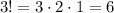 
Таким образом, всего имеется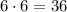 
недопустимых расстановок.
Значит, допустимых расстановок имеется:
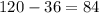
ответ: 84
√0.16+³√0.001 = 0.4+0.1 = 0.5