Відповідь: 8*5=40
Пояснення:
y = f(x)
Сначала осознаем как должен выглядеть график (рис. 1):
Рисуем прямые x = -5 и x = 6, график не должен выходить за эти прямые (обозначили область определения).Рисуем прямые y = -4 и y = 3, график не должен выходить за эти прямые (обозначили множество значений).На оси Ox отмечаем интервал (1;4), график функции должен проходить через ось Ox в этом интервале (обозначили промежуток нулевого значения).Теперь построим график функции (рис. 2):
Для простоты построим график ломанной (она непрерывна и просто изображается).
Функция убывает на всей области определения, поэтому для самого меньшего х из области определения , должно быть самое наибольшее y из множества значений (потом это значение уже не реализуется т.к. функция убывает, тогда множество значений будет другим). Итог: вершина ломанной в точке (-5;3).Пусть следующая вершина в точке (0;2).Ноль функции, он же пусть будет и вершиной ломанной, в точке (3;0) т.к. 3 ∈ (1;4).Последняя вершина в точке (6;-4), y= -4 для нужного множества значений.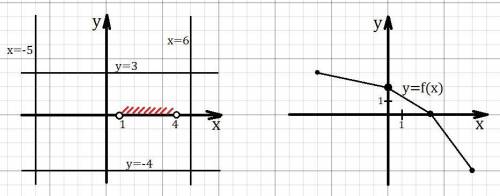
у = 5х - 3
Точка А (0; -3)
5 · 0 - 3 = -3
-3 = -3
Точка А (0; -3) принадлежит графику функции у = 5х - 3.
Точка В (-1; -4)
5 · (-1) - 3 ≠ -4
-5 - 3 ≠ -4
-8 ≠ -4
Точка В (-1; -4) не принадлежит графику функции у = 5х -3.
Точка С (0; -3)
5 · (-2) - 3 = -13
-13 = -13
Точка С (-2; -13) принадлежит графику функции у = 5х -3.
Точка М (3; 12)
5 · 3 - 3 = 12
15 - 3 = 12
12 = 12
Точка М (3; 12) принадлежит графику функции у = 5х -3.
Точка Е(0,2; -2)
5 · 0,2 - 3 = -2
1 - 3 = -2
-2 = -2
Точка Е(0,2; -2) принадлежит графику функции у = 5х -3.
Точка К (-0,4; -1)
5 · (-0,4) - 3 ≠ -1
-2 - 3 ≠ -1
-5 ≠ -1
Точка В (-0,4; -1) не принадлежит графику функции у = 5х -3.
Обобщённый ответ: графику функции у = 5х -3 принадлежат точки А(0;-3), С(-2;-13), М(3;12) и Е(0,2;-2).
5•8=40
Объяснение:
множник-множник=добуток. (5•8=40)