За 2 кг персиков и 2,5 кг абрикосов заплатили 80 грн.. При сезонном изменении цен персики подешевели - id1339192820230606 от COCOBAKUOFFICI 06.06.2023 02:58

Question

Алгебра: За 2 кг персиков и 2,5 кг абрикосов заплатили 80 грн.. При сезонном изменении цен персики подешевели на 30 %, а абрикосы подорожали на 20 %. В результате вся покупка подешевела на 5 %. Сколько стоит 1 кг абрикосов после подорожания?

COCOBAKUOFFICI · Accepted Answer

Стандартные решения через дискриминант уже написаны, можно по ним свериться. Предложу "быстрые", но которые не всегда срабатывают.

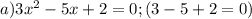a) 3x^2-5x+2=0; (3-5+2=0) - видно, что сумма коэффициентов в этом квадратном уравнении равна 0. Корни находятся быстро и безболезненно.

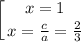
$$\left [ {{x=1} \atop {x=\frac{c}{a}=\frac{2}{3} }} \right.$

ответ: 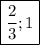$\boxed{\frac{2}{3};1 }$

б) тут действительно проще всего выделить полный квадрат. С опытом приходит их видение.

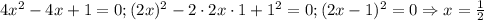
$4x^2-4x+1=0; (2x)^2-2\cdot 2x\cdot 1+1^2=0; (2x-1)^2=0 \Rightarrow x=\frac{1}{2}$

ответ: 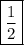$$\boxed{\frac{1}{2} }$

в) 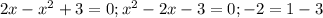2x-x^2+3=0; x^2-2x-3=0; -2=1-3

Здесь 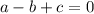a-b+c=0 или проще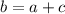 b=a+c

В этом случае

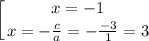
$$\left [ {{x=-1} \atop {x=-\frac{c}{a}=-\frac{-3}{1}=3 }} \right.$

ответ: 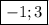$\boxed{-1;3}$

P.S. как видим, ни разу не был вычислен дискриминант. И примеров таких уравнений довольно много, в том числе и на экзаменах. Поэтому советую запомнить эти частные случаи и тренироваться побольше.

MOGZ ответил