кубическая функция может иметь только локальный минимум. Потому что при х ->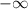 
она уходит в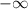
точки минимума и максимума соответствуют нулям производной
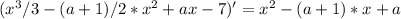
сумма степеней равна нулю, значит один корень = 1, второй = a
локальным минимумом является больший корень (кубическая функция возрастает от минус бесконечности до первого корня, потом убывает, потом снова возрастает до плюс бесконечности)
значит при a<1 локальный минимум f(x=1) = 1/3 - (a+1)/2 + a - 7 = a/2 - 7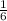 
при а>1 локальный минимум f(x=a) = a^3/3-(a+1)/2*a^2+a^2 - 7 = (1/3 - 1/2) a^3 + (-1/2+1) a^2 - 7 = - a^3 / 6 + a^2 / 2 - 7
при a = 1 имеем точку перегиба и никакого минимума
0,1^2*800+(1/9)^2*27= (1/10)^2*800+1/81*27=1/100*800+1/3=8+1/3=25/3=8*1/3 здесь ответ:
8 пишешь в фиолетовую рамку а в зелёную 1 и 3
2. z*z^42, z^38*z^5, z^43*z^0 это правильные утверждения
3. (c^2)^5*c^4÷c^5=c^9
4. -x^13
5. -26,56c+2k