fmin = -1
Объяснение:
Необходимое условие экстремума функции одной переменной.
Уравнение f'0(x*) = 0 - это необходимое условие экстремума функции одной переменной, т.е. в точке x* первая производная функции должна обращаться в нуль. Оно выделяет стационарные точки xс, в которых функция не возрастает и не убывает.
Достаточное условие экстремума функции одной переменной.
Пусть f0(x) дважды дифференцируемая по x, принадлежащему множеству D. Если в точке x* выполняется условие:
f'0(x*) = 0
f''0(x*) > 0
то точка x* является точкой локального (глобального) минимума функции.
Если в точке x* выполняется условие:
f'0(x*) = 0
f''0(x*) < 0
то точка x* - локальный (глобальный) максимум.
Находим первую производную функции:
y' = 2·x-2
Приравниваем ее к нулю:
2·x-2 = 0
x1 = 1
Вычисляем значения функции на концах отрезка
f(1) = -1
f(0) = 0
f(4) = 8.00000000000000
ответ: fmin = -1, fmax = 8
Сначала построим графики обеих функций: параболы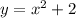 и обычной прямой
и обычной прямой  (чертеж смотрите ниже). Точками пересечения будут являться
(чертеж смотрите ниже). Точками пересечения будут являться 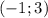 и
и 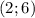 (для того, чтобы их найти, просто решим квадратное уравнение
(для того, чтобы их найти, просто решим квадратное уравнение 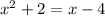 или же
или же 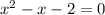 теоремой Виета).
теоремой Виета).
Чтобы найти искомую площадь, мы найдем площадь под графиком (выделено светло-голубым и желтым цветом) и площадь обведенной серым трапеции. После из второго вычтем первое и получим то, что нам нужно.1). Площадь трапеции.
2). Площадь под графиком.
Нам понадобится следующая формула (Ньютона-Лейбница):
Мы будем искать площадь на отрезке![[-1;2]](/tpl/images/1340/8031/7696d.png) :
:
3). Разность - искомая площадь.
Задача решена!