Чтобы найти среднюю скорость автомобиля, нужно весь путь, который проехал автомобиль, разделить на всё время, которое он был в пути.
Первые два часа автомобиль ехал со скоростью 70 км/ч. Значит он проехал 70*2=140 (км)
Затем пять часов автомобиль ехал со скоростью 90 км/ч. Значит он проехал 5*90=450 (км)
В конце пути автомобиль один час ехал со скоростью 60 км/ч. Значит он проехал 1*60=60(км)
140+450+60=650 (км) - весь путь, который проехал автомобиль.
2+5+1=8 (часов) - всё время, которое автомобиль был в пути.
Vсред. = 650:8 = 81,25 (км/ч)
ответ: средняя скорость автомобиля на протяжении всего пути 81,25 км/ч.
![+ , - , \cdot , : , x^n , \sqrt[n]{x} и \log_a{x}](/tpl/images/0480/8307/7c93b.png) – имеют ОДНОЗНАЧНЫЙ результат. Вы, возможно знаете пока не все из них, но это не меняет ничего в рассуждениях. Однозначность действия означает, что при вычислении результата любого из них получается однозначный ответ. Ну, например, ведь нет такого, что у одного при вычислении
– имеют ОДНОЗНАЧНЫЙ результат. Вы, возможно знаете пока не все из них, но это не меняет ничего в рассуждениях. Однозначность действия означает, что при вычислении результата любого из них получается однозначный ответ. Ну, например, ведь нет такого, что у одного при вычислении 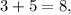 а у другого
а у другого 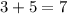 :–) ?! Конечно же, нет, это бы вызывало полную неразбериху и ни в одной науке ничего нельзя было бы вычислить ни по одной формуле. Но иногда, при изучении квадратного корня, учащиеся понимают это действие не совсем корректно, полагая, что
:–) ?! Конечно же, нет, это бы вызывало полную неразбериху и ни в одной науке ничего нельзя было бы вычислить ни по одной формуле. Но иногда, при изучении квадратного корня, учащиеся понимают это действие не совсем корректно, полагая, что 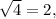 но одновременно с тем как бы и
но одновременно с тем как бы и 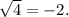 Это ошибка! Так понимать действие корня нельзя. Любой калькулятор покажет именно
Это ошибка! Так понимать действие корня нельзя. Любой калькулятор покажет именно 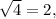 и это и есть верный результат вычислений, поскольку он единственный, так как любое арифметическое действие должно давать ОДНОЗНАЧНЫЙ результат.
и это и есть верный результат вычислений, поскольку он единственный, так как любое арифметическое действие должно давать ОДНОЗНАЧНЫЙ результат.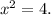 Корни этого нелинейного уравнения, как легко понять:
Корни этого нелинейного уравнения, как легко понять:  и
и 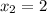 или в короткой записи
или в короткой записи 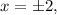 что равносильно
что равносильно 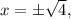 где сам «арифметический квадратный корень»
где сам «арифметический квадратный корень» 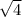 – это именно ПОЛОЖИТЕЛЬНОЕ число, а уж перед ним ставятся разные знаки, чтобы показать, что «корнями этого нелинейного уравнения» являются и само значение «квадратного арифметического корня» и число, противоположное ему. Аналогично, например, для уравнения:
– это именно ПОЛОЖИТЕЛЬНОЕ число, а уж перед ним ставятся разные знаки, чтобы показать, что «корнями этого нелинейного уравнения» являются и само значение «квадратного арифметического корня» и число, противоположное ему. Аналогично, например, для уравнения: 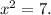 Корни этого нелинейного уравнения, как легко понять:
Корни этого нелинейного уравнения, как легко понять: 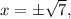 где сам «арифметический квадратный корень»
где сам «арифметический квадратный корень» 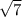 – это именно ПОЛОЖИТЕЛЬНОЕ число, а уж перед ним ставятся разные знаки, чтобы показать, что «корнями этого нелинейного уравнения» являются и само значение «квадратного арифметического корня» и число, противоположное ему.
– это именно ПОЛОЖИТЕЛЬНОЕ число, а уж перед ним ставятся разные знаки, чтобы показать, что «корнями этого нелинейного уравнения» являются и само значение «квадратного арифметического корня» и число, противоположное ему.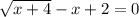 ;
;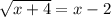 ;
;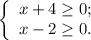
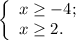
![x \in [ 2 ; +\infty ]](/tpl/images/0480/8307/22de1.png) ;
;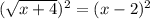 ;
;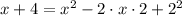 ;
;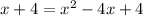 ;
;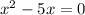 ;
;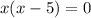 ;
;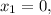 это не соответствует ОДЗ, поскольку
это не соответствует ОДЗ, поскольку ![x_1 = 0 \notin [ 2 ; +\infty ]](/tpl/images/0480/8307/72ba8.png) ;
;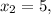 что соответствует ОДЗ, поскольку
что соответствует ОДЗ, поскольку ![x_2 = 5 \in [ 2 ; +\infty ]](/tpl/images/0480/8307/2f42f.png) ;
;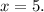
N1.
1)
Раскрываем скобки.
3,6y + 16,2 - 0,6y^2 - 2,7y = 0
-0,2y^2 + 0,9y + 16,2 = 0 | : -3
(Делим все на -3)
0,2y^2 - 0,3y - 5,4 = 0
Это квадратное уравнение. Ищем корни через Дискриминант. Для простоты домножим все на 10
2y^2 - 3y - 54 = 0
D = b^2 - 4ac
D = 9 - 4(2 * (-54)) = 9 + 432 = 441 = 21^2
x1 = (3 - 21) / 2 * 2 = -18/4 = -4,5
x2 = (3 + 21)/ 2 * 2 = 24/4 = 6
2)
|2x - 5| = 5
Раскрываем модуль (+ -)
2x - 5 = 5 (При 2x - 5 > 0)
2x - 5 = -5 (При 2x - 5 < 0)
2x = 10; x = 5
2x = 0; x = 0
3)
9x^2 = 49
Извлекаем квадратный корень.
3x = 7
x = 7/3
4)
Тут понадобится знание следующих формул.
x^2 - y^2 = (x - y)(x + y) (Разность квадратов)
(x + y)^2 = x^2 + 2xy + y^2 (Квадрат суммы)
Раскрываем скобки и формулы.
x^2 - 4 = 3(x^2 + 8x + 16) - 2x^2 - 10x
(x^2 - 3x^2 + 2x^2) + (10x - 24x) = 48 + 4
-14x = 52
7x = -26
x = -26/7 (странный ответ, но по сути все верно)
N2.
1) Тут все просто. Когда что-то в степень возводится в степень, то степени перемножаются. Прим. (x^3)^2 = x^6
-a^15 * b^30 * 5ab
-5a^16 * b^31
2)
(x - y)^2 = x^2 - 2xy + y^2 (Квадрат разности)
Раскрываем скобки, используем формулу квадрата разности.
(64p^2 - 16pq + q^2) - (64p^2 + 12pq - 16pq - 3q^2)
(64q^2 - 64q^2) + (-16pq - 12pq + 16pq) + (q^2 + 3q^2)
4q^2 - 12pq
Еще и 4q для красоты вынести можно.
4q(q - 3p)
N3.
Не уверен, что правильно понял задание. Если нужно найти точки пересечения функции, то делаем следующие.
Т.к. y без коэффициента (чисты, просто y), то можем приравнять одно к другому.
-2x + 1 = x + 4
-3 = 3x
x = -1
Это точка пересечения по оси абсцисс (по x). Теперь ищем по оси ординат (по y). Для этого поставим найденное значение x в любое уравнение (допустим в (2).
y = -1 + 4
y = 3
Точка пересечения найдена)
x = -1; y = 3
(-1; 3)
N4
Выражаем y из (2)
y = 5 - 2x
Подставляем в (1)
3x - 5(5 - 2x) = 1
3x - 25 + 10x = 1
13x = 26
x = 2
Подставляем в (2), ищем y
y = 5 - 4
y = 1
Все)
x = 2; y = 1
Дальше текстовые задачи, а я за Украинский не шарю, извиняй. Да и время щас поджимает, т.ч. все равно не успел бы. N8 на бумаге решил.
P.s. Извини, что так долго, отвлекали) Дай лучшего, если не сложно. Понимаю, что 3 задачи не решил, но все же, работа немалая) Если будут вопросы - пиши ;)
p.p.s. Там на листе не a = 12, а AB = 12 (думаю и так понятно, но все же).