а)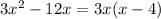 
б)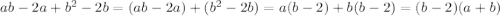 
или
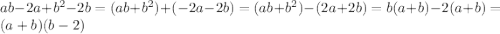
в)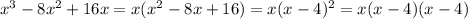 
или
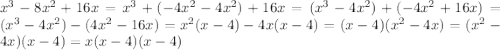
Наречия на -о (-е), образованные от качественных имен прилагательных, имеют две степени сравнения: сравнительную и превосходную.
Сравнительная степень наречий имеет две формы и составную форма сравнительной степени образуется с суффиксов -ее (-ей), -е, -ше от исходной формы наречий, от которой отбрасываются конечные -о (-е), -ко.
Составная форма сравнительной степени наречий образуется путем сочетания наречий и слов более и менее.
Превосходная степень наречий имеет, как правило, составную форму, которая представляет собой сочетание двух слов — сравнительной степени наречия и местоимения всех (всего).
Во-первых, отметим, что аргументы логарифмов должны быть строго больше нуля, но поскольку аргументы -- целые числа, то они должны быть хотя бы 
. С другой стороны, как нетрудно заметить, их сумма равна 
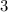. Стало быть, каждый из них равен единице: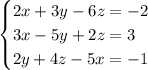 
Детерминант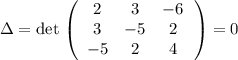 
(-(1 строка) - (2 строка) = (3 строка)). Решение можно параметризовать: 
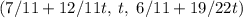, откуда 
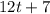должно делиться на 
, а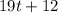 
должно делиться на 
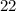. Тогда 
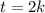, потому 
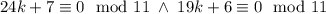. Из первого 
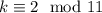, а из второго -- 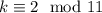. Итак, 
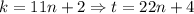, поэтому решение переписывается в виде 
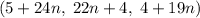. Итак, слева у исходного неравенства стоит нуль, а справа -- 
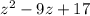. Получаем, что 
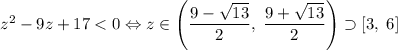, а потому подходит только 
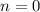и соответствующая тройка 
.
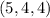а) 3Х^2-12Х = 3Х(Х-4)
б) ав-2а+в^2-2в = (ав-2а)+(в^2-2в) = а(в-2)+в(в-2) = (а+в)(в-2)
в) х^3-8х^2+16х = х(х^2-8х+16)-это формула сокращенного умножения=х(х-4)^2 скобка в квадрате=х(х-4)(х-4)