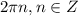Она не имеет 3 решения, потому что ее максимум это только 2 решения, так как первое это уравнение окружности , а вторая прямой, тогда она может пересечь окружность только в двух точках !
Одно решение она имеет
Либо можно думать так как это окружность с радиусом √3 и , и так как она должна касаться только в одной точке, а это может быть когда это точка касания радиуса, и теперь можно разделить осями и самой прямой прямоугольный треугольник , и она будет иметь стороны a и a . Тогда гипотенуза √a^2+a^2=a√2 и она должна равняться радиусу то есть высота будет равна a^2/a√2=a/√2 тогда нужно приравнять a/√2 = √3 a=√6
1. Область определения функции — множество всех действительных чисел.
2. Множество значений функции:
Так как синус изменяется от -1 до 1, то оценивая в виде двойного неравенства, имеем
Множество значений функции y=-2sinx: отрезок [-2;2].
3. Функция периодическая с периодом T = 2π
4. Функция нечетная , так как y(-x) = 2sin x = -y(x)
5. Наибольшее значение, равное 2, при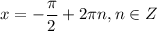
Наименьшее значение, равное -2, при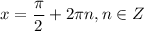
6. Функция возрастает на отрезке![\bigg[-\dfrac{3\pi}{2};-\dfrac{\pi}{2}\bigg]](/tpl/images/0199/1232/9b9b9.png)
и на отрезках, получаемых сдвигами этого отрезка на 
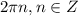
убывает на отрезке![\bigg[-\dfrac{\pi}{2};\dfrac{\pi}{2}\bigg]](/tpl/images/0199/1232/aa45e.png)
и на отрезках, получаемых сдвигами этого отрезка на 