tg2x-sec2x
Объяснение:
умножим числитель и знаменатель первой дроби на sinx-cosx
тогда числитель (sinx-cosx)²,знаменатель sinx²-cosx²
Раскроем числитель по ФСУ тогда sinx²+cosx²-2sinxcosx, а в знаменателе вынесем -1, тогда cosx²-sinx² по ОТТ и формуле двойного угла для синуса числитель равен 1-sin2x, а знаменатель по формуле двойного угла для косинуса равен -cos2x. Почленно поделим на -cos2x, тогда получим tg2x-1/cos2x, по определению, величина обратная косинусу есть секанс, окончательно получаем tg2x-sec2x
1)
По теореме Виета для уравнения 4х²-6х-1 :
х1+х2 = 1.5
х1*х2 = -0.25
2)
По теореме Виета для нового уравнения :
В = -(у1+у2) = -((2/х1³)-1 +(2/х2³)-1) = 578
С = -(у1*у2) = ((2/х1³)-1)*((2/х2³)-1) = 321
Уравнение : y²+578y+321 = 0
ответ : у²+578у+321 = 0
P.S если интересно как я из -((2/х1³)-1 +(2/х2³)-1) получил 578, то я сейчас примерно покажу (для удобства пусть х1 будет х, а х2 будет у) :
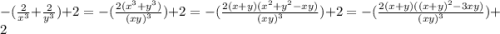
Ну и уже по теореме Виета (х+у = 1.5, х*у = -0.25) я подставил значения и решил, с умножением там примерно тоже самое)
Для доказательство просто рассмотрим два случая: когда - нечетное и когда
- нечетное и когда  - четное.
- четное.
1). - нечетное, то есть
- нечетное, то есть  .
.
При всех нечетных натуральных число
число 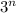 имеет остаток
имеет остаток  при делении на
при делении на 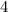 .
.
Доказать это можно таким образом: приТакже, при любом натуральном значении число
число  имеет остаток
имеет остаток  при делении на
при делении на 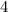 .
.
Так происходит, потому что само числоТретье слагаемое: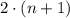 будет нацело делиться на
будет нацело делиться на 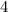 :
:
Значит, если - нечетное, то:
- нечетное, то:
При нечетных все, как видите, сходится.
все, как видите, сходится.
2). - четное, или же
- четное, или же 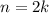 .
.
Как мы определили ранее, в этом случае и
и 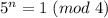 .
.
При этом второе слагаемое:
Найдем всю сумму:
И при четных утверждение работает.
утверждение работает.
Как известно, каждое натуральное число либо четное, либо нечетное (третьего не дано) и никаких других натуральных чисел, которые не являются четными и не являются нечетными одновременно, науке неизвестно.
Так что мы рассмотрели все случаи, и в каждом из них результат был равен , то есть делился на
, то есть делился на 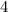 .
.