нужно решить уравнения по алгебре нужно решить уравнения по алгебре нужно решить уравнения по алгебре нужно решить уравнения по алгебре нужно решить уравнения по алгебре нужно решить уравнения по алгебре. ">

👇

Увидеть ответ

Ответ:

urkashkz777

05.04.2022

Решение смотреть во вложении нужно решить уравнения по алгебре. ">

4,8(88 оценок)

Открыть все ответы

Ответ:

andrei822

05.04.2022

ответ: (2;3) ,( 3;2)

Объяснение:

Для удобства пусть:

НОД (a,b)= t

a=n*t

b=m*t

m,n -взаимнопростые натуральные числа.

Тогда из взаимной простоты m и n следует что :

НОК (a,b) =n*m*t

t+n*m*t= m*t +n*t +2

t*( 1+n*m -m-n)=2

t*(m-1)*(n-1)=2

Для t возможно два варианта : t=1 ; t=2

1) t=2

(m-1)*(n-1)=1

Поскольку : m-1>=0 и n-1>=0 , то

n-1 =m-1=1

n=m=2 , но n и m взаимнопростые , поэтому данный случай нам не подходит.

2) t=1

(m-1)*(n-1)=2

m-1=2 → m=b=3

n-1=1 → n=b=2

Аналогично при симметричной ситуации:

b=2

a=3

P.S подробнее поясню почему n=m=t=2 не подходит.

В этом случае : a=b=4

НОК (4 ;4)= НОД (4;4)=4

4 +4 = 4+4+2 (неверно)

4,6(25 оценок)

Ответ:

Котик132457

05.04.2022

1) y=sin x, y=cos x, x=-5π/4, x=π/4.
Заданный отрезок графиками функций разбивается на 2 участка: левая часть - от заданного предела x=-5π/4 до точки встречи графиков, где график функции синуса выше графика косинуса.
Направо от этой точки график синуса выше графика косинуса.
Это определяет площадь как сумма интегралов разностей функций.
Точка встречи - это значение (-π+(π/4)) = -3π/4.
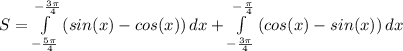$S= \int\limits^{- \frac{3 \pi }{4} }_{- \frac{5 \pi }{4} } {(sin(x)-cos(x))} \, dx + \int\limits^{- \frac{ \pi }{4} }_{- \frac{3 \pi }{4} } {(cos(x)-sin(x))} \, dx$ .
Значения аргумента в заданных пределах:
-1.25π = -3.92699,
-0.75π = -2.35619,
0.25π = 0.785398.
Значения функции синуса в заданных пределах:
0.707107, -0.70711, 0.707107. (это +-√2/2)
Значения функции косинуса в заданных пределах:
-0.70711, -0.70711, 0.707107. (это +-√2/2)
Значения функции косинуса в заданных пределах:
Площадь равна 1.414214 + 2.828427 = 4.242641 = 3√2.

2) y=-x^2-2x+4, y=-x^2+4x+1, y=5.
Заданный отрезок графиками функций разбивается на 2 участка, граничные точки которых надо определить.
Средняя точка - равенство функций y=-x^2-2x+4, y=-x^2+4x+1.
-x^2 - 2x + 4 = -x^2 + 4x + 1,
6х = 3,
х = 3/6 = 1/2.
Левая точка - равенство y=-x^2-2x+4, y=5
-x^2 - 2x + 4 = 5.
-x^2 - 2x -1 = 0.
Квадратное уравнение, решаем относительно x: Ищем дискриминант:
D=(-2)^2-4*(-1)*(-1)=4-4*(-1)*(-1)=4-(-4)*(-1)=4-(-4*(-1))=4-(-(-4))=4-4=0; Дискриминант равен 0, уравнение имеет 1 корень:
x=-(-2/(2*(-1)))=-(-2/(-2))=-(-(-2/2))=-(-(-1))=-1.
Правая точка - равенство y=-x^2+4x+1, y=5.
-x^2 + 4x + 1 = 5.
-x^2 + 4x - 4 = 0.
Квадратное уравнение, решаем относительно x: Ищем дискриминант:
D=4^2-4*(-1)*(-4)=16-4*(-1)*(-4)=16-(-4)*(-4)=16-(-4*(-4))=16-(-(-4*4))=16-(-(-16))=16-16=0; Дискриминант равен 0, уравнение имеет 1 корень:
x=-4/(2*(-1))=-4/(-2)=-(-4/2)=-(-2)=2. Линия у = 5 находится выше парабол.
Площадь равна:
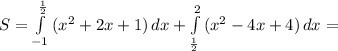
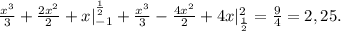
$S= \int\limits^{ \frac{1}{2} }_{-1} {(x^2+2x+1)} \, dx + \int\limits^2_{ \frac{1}{2} } {(x^2-4x+4)} \, dx =$ $\frac{x^3}{3}+ \frac{2x^2}{2}+x|_{-1}^{ \frac{1}{2} }+ \frac{x^3}{3}- \frac{4x^2}{2}+4x|_{ \frac{1}{2} }^2= \frac{9}{4}=2,25.$