Объяснение:
ответ на фото.............

Начнем с ОДЗ:
3x+6 > 0 => x > -2
2x - 4 > 0 => x > 2. Общее ОДЗ: x>3
2x - 6 > 0 => x > 3
Представим 2, как log1/2 (1/4), чтобы было удобнее считать. Далее применяем свойства суммы и разности логарифмов, и неравенство сводится к обычному дробно-рациональному. И не забываем поменять знак на противоположный, потому что основание логарифма меньше 1.
log1/2 ( (3x+6)/(2x-4) ) < log1/2 ( 1/4*(2x-6) )
log1/2 t - убывающая функция, а значит знак меняем.
(3x+6)/(2x-4) > x/2 - 6/4
(3x + 6 -x² + 2x + 3x -6) / 2(x-2) > 0
x(8 - x) / 2(x-2) > 0
Решение этого неравенства будет x ∈ ( - ∞; 0) ∪ ( 2; 8)
Из ОДЗ следует, что х>3, то ответ будет: x ∈ ( 3; 8)
ответ: (3; 8)
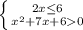
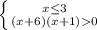
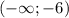 и
и 
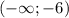 и
и ![(-1;3]](/tpl/images/0188/5648/df8ed.png)

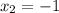
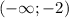 и
и 
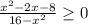
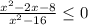
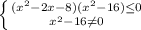
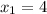

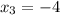
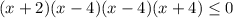
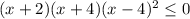
![(-4;-2]](/tpl/images/0188/5648/eac16.png)
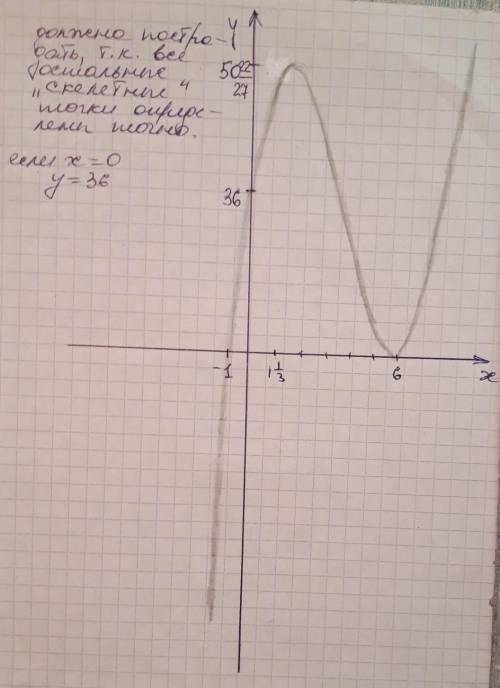
Исследовать функцию и построить график.