В решении.
Объяснение:
Даны точки B (-3;-4) и C(6;3).
1) Проходит ли график функции y = 19/x через точку C?
Нужно в уравнение подставить известные значения х и у (координаты точки). Если левая часть равна правой, то проходит, и наоборот.
y = 19/x; C(6;3);
3 = 19/6
3 ≠ 3,2, не проходит;
y = 19/x; B (-3;-4);
-4 = 19/-3
-4 ≠ -6,3, не проходит.
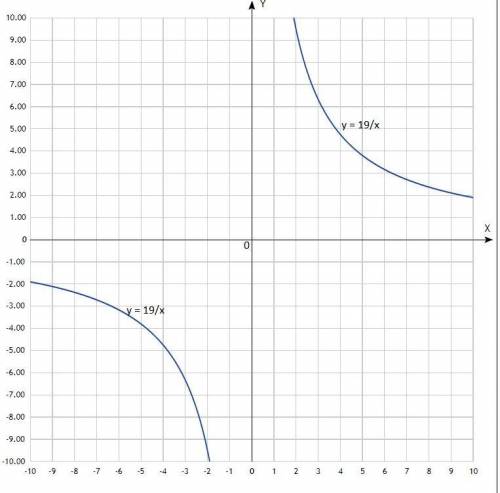
2) Построить график.
График - гипербола.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
Таблица:
х -10 -8 -6 -4 -2 -1 0 1 2 4 6 8 10
у -1,9 -2,4 -3,2 -4,8 -9,5 -19 - 19 9,5 4,8 3,2 2,4 1,9
По вычисленным точкам построить график.
1)область визначення множина дійсних чисел (симетрична відносно початку координат)
y(-x)=5(-х)²+1=5х²+1=y(x) - значить дана функція парна за означенням парної функції
2) область визначення множина дійсних чисел (симетрична відносно початку координат)
y(-x)=(-х)⁵+3(-х)³-(-х)=-х⁵-3х³+х=-(х⁵+3х³-х)=-y(x) значить дана функція непарна за означенням непарної функції
3) область визначення множина дійсних чисел (симетрична відносно початку координат)
y(1)=2*1⁴-1³+1=2-1+1=2
y(-1)=2*(-1)⁴-(-1)³+1=2+1+1=4
y(1)не дорівнює y(-1), значить функція не є парною
y(1) не дорівнює -y(-1), значить функція не є не парною
значить дана функція ні парна, ні непарна
4) область визначення множина дійсних чисел, за виключенням точки 0 (симетрична відносно початку координат)
y(-x)=3(-х)-2/(-х)=-3x+2/x=-(3x-2/x)=-y(x) значить дана функція непарна за означенням непарної функції
5) область визначення множина дійсних чисел (симетрична відносно початку координат)
y(1)=4*1²+[1]=4+1=5
y(-1)=4(-1)²+[-1]=4-1=3
y(1)не дорівнює y(-1), значить функція не є парною
y(1) не дорівнює -y(-1), значить функція не є не парною
значить дана функція ні парна, ні непарна