ответ:
если ветви параболы напрвлены вверх, то a> 0, вниз - a< 0.
при х=0, у=с, т. е нужно посмотреть, в какой точке парабола пересекает ось оу, если выше оси ох, то с> 0, ниже - с< 0.
осталось определить знак b. координата вершины параболы по оси ох х=-b/(2a).
если вершина параболы находится правее оси оу (x> 0) при a> 0 (ветви параболы напрвлены вверх) , b< 0, при a< 0 (ветви направлены вниз) b> 0.
если вершина параболы находится левее оси оу (xб0) при a> 0 (ветви параболы напрвлены вверх) , b> 0, при a> 0 (ветви направлены вниз) b< 0
объяснение:
всё
(-5; 1; 1)
Объяснение:
Найдём уравнение прямой, перпендикулярной данной плоскости и проходящей через точку A. Направляющим вектором данной прямой является вектор нормали плоскости, то есть вектор {3; 2; 2}. Составим каноническое уравнение прямой:
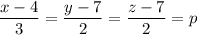
Из этого уравнения составим параметрическое уравнение:
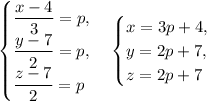
Чтобы найти точку пересечения прямой с плоскостью, то есть проекцию данной точки, подставим координаты из параметрического уравнения в уравнение плоскости:
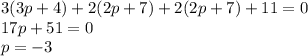
Подставляя найденное значение параметра, получим координаты искомой точки:
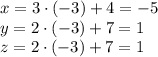
г) 3
Объяснение:
9156423/3=3052141