Объяснение:
1)Найти координаты вершины параболы:
а) y=x²-7x+10
х₀= -b/2a =7/2=3,5
у₀=3,5²-7*3,5+10=12,25-24,5+10= -2,25
Координаты вершины параболы (3,5; -2,25)
б)y= -2x²+3x+5
х₀= -b/2a= -3/-4=0,75
у₀= -2*0,75²+5*0,75+5= -2*0,5625+2,25+5= -1,125+2,25+5=6,125
Координаты вершины параболы (0,75; 6,125)
2)Найти координаты точек пересечения функции с осями координат:
а) y= -x²+5x-1
При пересечении графика с осью У х=0:
х=0
у= -0²+5*0-1
у= -1
Координаты пересечения графика с осью У (0; -1)
Для определения точек пересечения с осью Х (график парабола) нужно решить квадратное уравнение:
-x²+5x-1 =0
х²-5х+1=0
х₁,₂=(5±√25-4)/2
х₁,₂=(5±√21)/2
х₁,₂=(5±4,6)/2
х₁=0,2
х₂=4,8
Координаты точек пересечения графиком оси Х, нули функции,
(0,2; 0) (4,8; 0)
б)y=5x²-7x+2
При пересечении графика с осью У х=0:
х=0
у=5*0²-7*0+2
у=2
Координаты пересечения графика с осью У (0; 2)
Для определения точек пересечения с осью Х (график парабола) нужно решить квадратное уравнение:
5x²-7x+2=0
х₁,₂=(7±√49-40)/10
х₁,₂=(7±√9)/10
х₁,₂=(7±3)/10
х₁=0,4
х₂= 1
Координаты точек пересечения графиком оси Х, нули функции,
(0,4; 0) (1; 0)
Общая схема исследования функции:
Найти ОДЗ и точки разрыва функции. Найти точки пересечения графика функции с осями координат. Провести исследование функции с первой производной, то есть найти точки экстремума функции и интервалы возрастания и убывания. Исследовать функцию с производной второго порядка, то есть найти точки перегиба графика функции и интервалы его выпуклости и вогнутости. Найти асимптоты графика функции: а) вертикальные, b) наклонные. На основании проведенного исследования построить график функции.1. Здесь функция ограничений не имеет, точек разрыва тоже не имеет, т.е. существует для всех действительных х. Область определения функции: D(f) = R
2. Точки пересечения с осями координат.
2.1. Точки пересечения с осью абсцисс
Чтобы найти точки пересечения с осью Ох, нужно принять y=0:
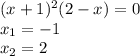
2.2. Точки пересечения с осью ординат.
Здесь нужно принять x=0 и подставив в функцию, получим y=2
3. Найдем производную функции
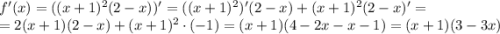
Приравниваем производную функции к нулю
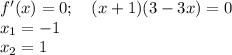
___-____(-1)____+___(1)_____-__
Функция возрастает на промежутке (-1;1), а убывает - (-∞;-1) и (1;+∞). В точке х=-1 производная функции меняет знак с (-) на (+), следовательно, точка х=-1 имеет локальный минимум, а в точке x=1 производная функции меняет с (+) на (-), имеем локальный максимум в точке х=1.
Найдем теперь вторую производную
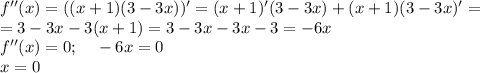
(0;2) - точка перегиба
Вертикальной асимптоты нет.
Поскольку предел f(x) и f(x)/x при х 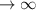 равен
равен 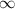 , то горизонтальной и наклонной асимптот нет.
, то горизонтальной и наклонной асимптот нет.
ответ: можно, при этом к=0, например, у=2.
Объяснение: