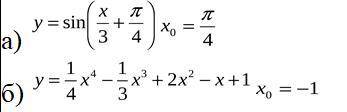
Найдите значение производной функции в заданной точке.

👇

Увидеть ответ

Ответ:

nikitasonar

12.07.2021

ответ: а) 1/6

Б) -7.

Объяснение:

Найдите значение производной функции в заданной точке.

4,7(82 оценок)

Открыть все ответы

Ответ:

Uliano4ka1

12.07.2021

a≤1⇒решений нет; a> 1⇒ 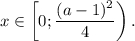$x\in\left[0;\dfrac{(a-1)^2}{4}\right).$

Объяснение:

Левая часть неравенства неотрицательна, поэтому при a≤0 решений нет.

Пусть a>0. Рассмотрим функцию 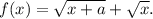$f(x)=\sqrt{x+a}+\sqrt{x}.$ Это возрастающая функция на своей области определения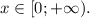 $x\in [0;+\infty).$

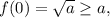Если $a\in(0;1],$ $f(0)=\sqrt{a} \ge a,$ а тогда в силу возрастания f(x)≥a на области определения, поэтому при таких a решений нет.

Пусть a>1. В этом случае 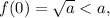$f(0)=\sqrt{a} < a,$ и нам нужно поймать момент, когда f(x) станет равен a. Итак, решаем уравнение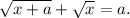 $\sqrt{x+a}+\sqrt{x}=a.$

Обозначим 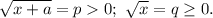$\sqrt{x+a}=p 0; \ \sqrt{x}=q\ge 0.$ Поскольку p²-q²=a, уравнение равносильно системе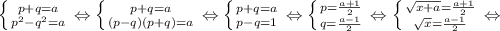 $\left \{ {{p+q=a} \atop {p^2-q^2=a}} \right. \Leftrightarrow \left \{ {{p+q=a} \atop {(p-q)(p+q)=a}} \right.\Leftrightarrow \left \{ {{p+q=a} \atop {p-q=1}} \right.\Leftrightarrow \left \{ {{p=\frac{a+1}{2}} \atop {q=\frac{a-1}{2}}} \right.\Leftrightarrow \left \{ {{\sqrt{x+a}=\frac{a+1}{2}} \atop {\sqrt{x}=\frac{a-1}{2}}} \right.\Leftrightarrow$

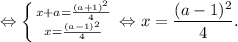$\Leftrightarrow \left \{ {{x+a=\frac{(a+1)^2}{4}} \atop {x=\frac{(a-1)^2}{4}}} \right.\Leftrightarrow x=\dfrac{(a-1)^2}{4}.$ Напомним еще раз, что функция f(x) возрастающая, поэтому слева от найденной точки функция меньше a, справа - больше a. Не забываем и про область определения.

4,5(96 оценок)

Ответ:

dssh70

12.07.2021

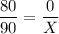$\displaystyle \frac{80}{90} = \frac{0}{X}$ .

Заученное без особого понимания "правило пропорции" говорит, что при данном равенстве неизвестная будет равна

$X = \dfrac{90\cdot 0}{80}$ , но это же нуль!

На самом деле "правило пропорции" - ничего более, чем умножение и деление. В самом деле, умножим обе части изначального уравнения на :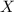

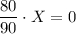$\dfrac{80}{90}\cdot X = 0$ .

Поделим на коэффициент перед неизвестной (или умножим на обратное ему число, что то же самое):

$X = \dfrac{90\cdot 0}{80}$ .

Пришли к результату, которое даёт нам "правило пропорции". Так в чём же проблема? А в самом первом шаге - умножении обеих частей на неизвестную .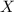

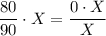$\dfrac{80}{90}\cdot X = \dfrac{0\cdot X}{X}$ .

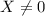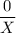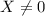Здесь, чтобы сократить неизвестную в правой части уравнения необходимо условие $X\neq 0$ , которое, на самом деле, уже предполагается при постановке задачи. Действительно, выражение $\dfrac{0}{X}$ имеет смысл только при озвученном условии $X\neq 0$ .

Но раз это так, то мы сразу же можем написать значение выражения справа в изначальном уравнении:

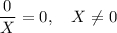
$\dfrac{0}{X} = 0,\quad X\neq 0$

И что же мы получим? Получим уравнение на 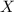, не зависящее от 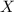, т.е. некоторое равенство, которое должно быть верно для любого значения неизвестной 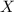. Посмотрим на него:

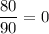$\dfrac{80}{90} = 0$ .

Не нужно иметь и семи пядей во лбу, чтобы догадаться, что полученное равенство не верно ни при каком значении 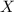. Отсюда делаем вывод, что изначальное уравнение решений не имеет.

ответ. 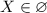$X\in\varnothing$ .

P.S. Фраза "посчитать пропорцию" вообще особого смысла в себе не имеет - можно с тем же успехом пытаться "считать" равенства или уравнения. Правда для данного случая счёт закончится довольно быстро - у нас всего 1 уравнение.

4,5(63 оценок)

Это интересно:

Семейная-жизнь

21.02.2020

Как справиться с ребенком, который постоянно говорит нет...

02.01.2020

Как стать серьезным: 10 советов от успешных людей...

Компьютеры-и-электроника

25.10.2022

Как словить покемона Кресселию...

Здоровье

22.01.2023