Для решения неравенства методом интервалов будем выполнять следующие шаги
1) найдем корни уравнения уравнения
(x+3)(x-4)(x-6)=0
произведение равно нуля когда любой из множителей равен нулю
х+3=0 или х-4=0 или х-6=0
тогда х= -3 или х= 4 или х=6
2) Нарисуем числовую ось и отметив полученные точки
-3 4 6
3) в каждом из полученных промежутков определим знак нашего выражения
при х< -3 проверим для точки х= -5
(-5+3)(-5-4)(-5-6)=(-)(-)(-) <0
при -3<x<4 проверим для точки х=0
(0+3)(0-4)(0-6)=(+)(-)(-)>0
при 4<x<6 проверим для точки х=5
(5+3)(5-4)(5-6)=(+)(+)(-)<0
при x>6 проверим для точки х=10
(10+3)(10-4)(10-6)= (+)(+)(+)>0
4) расставим полученные знаки над промежутками
--3+4-6__+
5) и теперь осталось выбрать промежутки где стоит знак "минус"
( по условию <0)
Запишем полученные промежутки (-∞; -3) ∪(4;6)
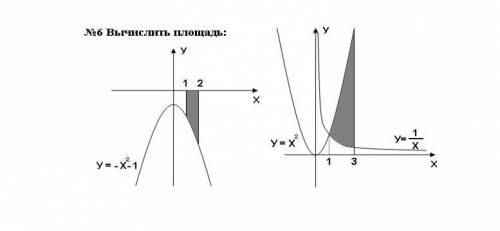
Чтобы вычислить площадь фигуры, ограниченной графиком функции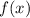 на заданном промежутке
на заданном промежутке ![[a; \ b]](/tpl/images/1350/2276/cd2bf.png) , следует найти определенный интеграл:
, следует найти определенный интеграл:
где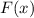 — первообразная для функции
— первообразная для функции 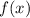
1) Имеем функцию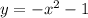 и следует вычислить площадь, которую она ограничивает на координатной плоскости на отрезке
и следует вычислить площадь, которую она ограничивает на координатной плоскости на отрезке ![[1; \ 2]](/tpl/images/1350/2276/2bc6a.png)
Найдем определенный интеграл, приписав перед ним знак "минус", поскольку график функции находится под осью абсцисс:
2) Вычислим площадь фигуры, ограниченной графиками функций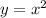 и
и 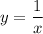 на отрезке
на отрезке ![[1; \ 3]](/tpl/images/1350/2276/24e94.png)
Чтобы найти эту площадь, следует вычислить определенный интеграл разности функций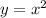 и
и 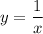 (только при такой разности площадей, образованных функциями на координатной плоскости, получим площадь фигуры, изображенной на рисунке):
(только при такой разности площадей, образованных функциями на координатной плоскости, получим площадь фигуры, изображенной на рисунке):
ответ: 1)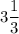 кв. ед.; 2)
кв. ед.; 2) 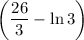 кв. ед.
кв. ед.