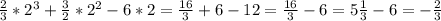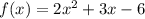Все функции - параболы вида
a - определяет "ширину" ветвей, при 0<а<1 ветви "шире", при а > 1 "уже"
При отрицательном а - ветви направлены вниз, при положительном вверх. В 3 и 4 примерах а = -1, поэтому ветки вниз
b - (в данных примерах не используется) показывает смещение вершины параболы вдоль оси OX, положительный левее, отрицательный правее от оси OY
с - смещение вершины графика вдоль оси OY - положительный с - выше, отрицательный ниже, при с=0 ветка графика пересекает точку 0,0
Объяснение:
ну в место 51 поставь 52
Объяснение:
Обозначим:
а - длина прямоугольника;
в - ширина прямоугольника
Согласно условия задачи,
2*(а+в)=40
а*в=51
Решим получившуюся систему уравнений, для этого из второго уравнения найдём значение (а) и подставим её значение в первое уравнение:
а=51/в
2*(51/в+в)=40
(102+2в²)/в=80
102+2в²=40в
2в²-40в+102=0 сократим на 2
в²-20в+51=0
в1,2=(20+-D/2*1
D=√(20²-4*1*51)=√(400-204)=√196=14
в1,2=(20+-14)/2
в1=(20+14)/2
в1=17 - не соответствует условию, т.к. для ширины большая величина
в2=(20-14)/2
в2=3 (см - ширина прямоугольника)
а=51/3
а=17 (см - длина прямоугольника)
ответ: в прямоугольнике длина - 17см; ширина 3см
Алгебра!.Дана функция: . Найдите F(2) 
-2/3
Объяснение:
f(x) = 2x ^2 +3x-6
F(x) =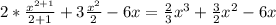
F (2) =