Выражение: (3*a-a^2)^2-a^2*(a-2)*(a+2)+2*a*(7+3*a^2)
ответ: 13*a^2+14*a
Решаем по действиям:
1. (3*a-a^2)^2=9*a^2-6*a^3+a^4
2. a^2*(a-2)=a^3-a^2*2
3. (a^3-a^2*2)*(a+2)=a^4-a^2*4
4. 9*a^2-6*a^3+a^4-(a^4-a^2*4)=9*a^2-6*a^3+a^4-a^4+a^2*4
5. a^4-a^4=0
6. 9*a^2+a^2*4=13*a^2
7. 2*(7+3*a^2)=14+6*a^2
8. (14+6*a^2)*a=14*a+6*a^3
9. -6*a^3+6*a^3=0
Решаем по шагам:
1. 9*a^2-6*a^3+a^4-a^2*(a-2)*(a+2)+2*a*(7+3*a^2)
2. 9*a^2-6*a^3+a^4-(a^3-a^2*2)*(a+2)+2*a*(7+3*a^2)
3. 9*a^2-6*a^3+a^4-(a^4-a^2*4)+2*a*(7+3*a^2)
4. 9*a^2-6*a^3+a^4-a^4+a^2*4+2*a*(7+3*a^2)
5. 9*a^2-6*a^3+a^2*4+2*a*(7+3*a^2)
6. 13*a^2-6*a^3+2*a*(7+3*a^2)
7. 13*a^2-6*a^3+(14+6*a^2)*a
8. 13*a^2-6*a^3+14*a+6*a^3
9. -6*a^3+6*a^3=0
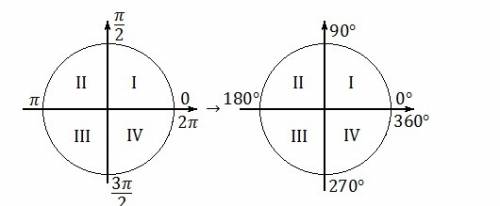
Для того чтобы ответить на этот вопрос нужно представить себе окружность, которую разделили на 4 части.
места "разрезов" как раз проходят через углы в 90°, 180°, 270°, 360°
Когда вы режете пиццу в какой кусок попадает разрез?
Правильно- ни в какой. То что между разрезами - то и попадает в кусок. А сами разрезы- остаются просто разрезами.
Таким образом
α ∈ (0°; 90°) ⇒ это угол I координатной четверти;
α ∈ (90°; 180°) ⇒ II координатная четверть;
α ∈ (180°; 270°) ⇒ III координатная четверть;
α ∈ (270°; 360°) ⇒ IV координатная четверть.
А сами углы 90°,180°, 270°, 360° сами по себе. Это границы.
y(x) = 2x - 2
1) A(1 ; 3)
3 = 2 * 1 - 2
3 = 0 - неверно
Эта точка не принадлежит графику этой функции
2) B(0 ; - 2)
- 2 = 2 * 0 - 2
- 2 = - 2 - верно
Эта точка принадлежит графику этой функции
3) C(2 ; 2)
2 = 2 * 2 - 2
2 = 2 - верно
Эта точка принадлежит графику этой функции
4) D(3 ; - 5)
- 5 = 2 * 3 - 2
- 5 = 4 - неверно
Эта точка не принадлежит графику этой функции
ответ : графику функции принадлежат точки B(0 ; - 2) и C(2 ; 2) .