первое число дает остаток 1 при делении на 4 значит куб первого числа при делении на 4 даст такой же остаток как и 1 в кубе, т.е как число 1*1*1=1 число 1 при делении на 4 дает остаток 1 итого куб первого числа при делении на 4 даст остаток 1
второе число дает остаток 3 при делении на 4 значит куб второго числа при делении на 4 даст такой же остаток как и 3 в кубе, т.е. как число 3*3*3=27 число 27 при делении на 4 дает остаток 3
сумма кубов первого и второго чисел при делении на 4 даст такой же остаток какой даст при делении на 4 сумма остатков чисел при делении на 4, т.е. как число 1+3=4, так как 4 при делении на 4 дает остаток 0, то сумма кубов этих чисел кратна 4 ---------------------------------- второй
так как первое число при делении на 4 дает остаток 1, то его можно записать в виде 4n+1, где n - некоторое целое число аналогично второе можно записать в виде 4k+3, где k - некоторое целое число
сумма кубов этих чисел а значит сумма кубов делится нацело на 4. Доказано
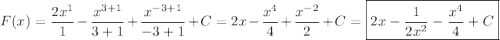
б).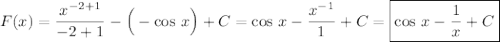
в).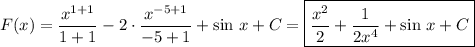
г).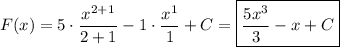
________________________Примечание.
В решении были использованы следующие правила:
Если