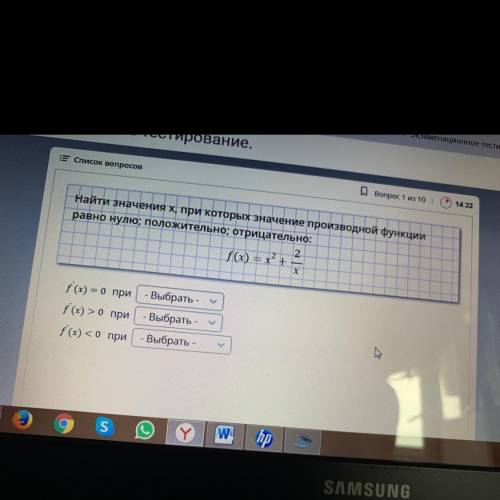
f'(x) = (x^2 + 2/x)' = 2x - 2/x^2
2x - 2/x^2 = 0
x - 1/x^2 = 0
(x^3 - 1) / x^2 = 0
x^3 - 1 = 0
x^3 = 1
x = 1
2x - 2/x^2 > 0
x - 1/x^2 > 0
(x^3 - 1) / x^2 > 0
x^3 - 1 = 0 ОДЗ: x^2 = 0
x^3 = 1 x = 0
x = 1
- 0 - 1 +
---○○>
x ∈ (1; +∞)
2x - 2/x^2 < 0
x - 1/x^2 < 0
(x^3 - 1) / x^2 < 0
x^3 - 1 = 0 ОДЗ: x^2 = 0
x^3 = 1 x = 0
x = 1
- 0 - 1 +
---○○>
x ∈ (-∞; 0) ∪ (0; 1)
ответ: f'(x) = 0 при x = 1
f'(x) > 0 при x ∈ (1; +∞)
f'(x) < 0 при x ∈ (-∞; 0) ∪ (0; 1)
Рассматривается выражение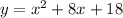 
Докажем, что y положительно при любом значении x. Допустим, что это не так. Найдём такие x, при которых y ≤ 0. Для этого решим неравенство:
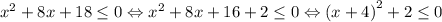
Или
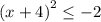
Что не имеет решений, так как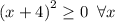 
Мы пришли к противоречию. Следовательно, 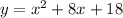принимает положительное значение при любых x.
Для нахождения наименьшего значения найдём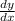 
:
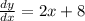
Приравняв его 0, найдём точку экстремума:
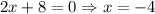
Убедимся, что найденная точка — действительно минимум.
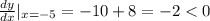
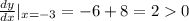
Итак, первая производная меняет в точке 
знак с "-" на "+", следовательно, в этой точке мы действительно имеем минимум.
Значение y при x = -4:
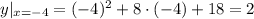
Логарифмическая — функция, обратная потенциированию.
Построив график обратной функции и зеркально отразив его относительно прямой y = x, получим нужный нам график.
Итак, обратная к
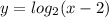
функция — это
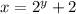
Строим график
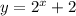
Его можно получить из графика
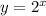
смещением вверх на 2 (либо смещением оси y вниз на 2).
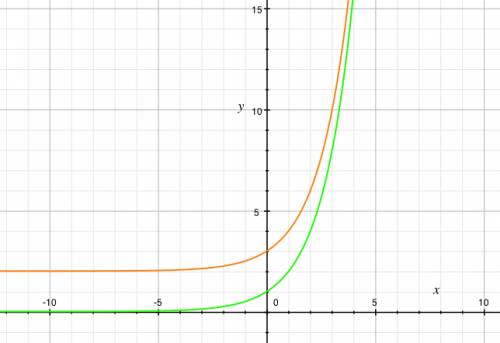
Это — быстровозрастающая функция, равная 1 при x = 0, стремящаяся к 0 на минус бесконечности. Располагается только в верхней полуплоскости (область значений y ≥ 0). Несколько точек для построения: x = 1, y = 2; x = 2, y = 4; x = 4, y = 16; x = -1, y = 0.5; x = -2, y = 0.25.
Рисунок 1 — графики функци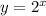й и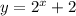
Отражением относительно прямой y = x получаем искомый график.
Рисунок 2 — графики функций 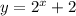и заданной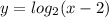
Объяснение:
f'(x)= 2x- 2/x²
2x- 2/x²=0
(x³-1)/x²=0
x=1
2x- 2/x²>0
(x³-1)/x²>0
x∈(1;+∞)
2x- 2/x²<0
x∈(-∞;0)∪(0;1)