Найдите область определения функции. ------------------------------------------------------------- Огромное распишите каждое действие в решении выражения, желательно через встроенную среду написания математики в знаниях. Кидать ответ с фотомача для набора - 1 звезда и жалоба. --------------------------------------------------------------
Первое, что можем заметить, это то, что выражение под корнем больше/равно нулю. Также замечаем, что знаменатель в дробовом выражении не может равняться нулю (Это записывать не нужно, так как будет включаться в решение неравенства).
Решим неравенство:
Отсюда имеем решение (значит и область определения):
|x-1|>|x+2|-3 |x-1|-|x+2|>-3 Раскроем модули. Приравняем каждое подмодульное выражение к нулю и найдем точки,в которых подмодульные выражения меняют знак: x-1=0 x+2=0 x=1 x=-2 Нанесем эти значения Х на числовую прямую:
(-2)(1)
Мы получили три промежутка.Найдем знаки каждого подмодульного выражения на каждом промежутке:
(-2)(1) x-1 - - + x+2 - + +
Раскроем модули на каждом промежутке: 1)x<-2 На этом промежутке оба подмодульных выражения отрицательны,поэтому раскрываем модули с противоположным знаком: -x+1+x+2>-3 3>-3 - неравенство верное при любых Х на промежутке x<-2
2) -2<=x<1 На этом промежутке первое подмодульное выражение отрицательное(его мы раскроем с противоположным знаком),а второе - положительное, и его мы раскроем с тем же знаком: -x+1-x-2>-3 -2x-1>-3 -2x>1-3 -2x>-2 x<1 С учетом промежутка -2<=x<1 получаем x e [-2;1)
3)x>=1 На этом промежутке оба подмодульных выражения положительные, поэтому раскрываем их без смены знака: x-1-x-2>-3 -3>-3 Неравенство не имеет решений на этом промежутке Соединим решения 1 и 2 промежутков и получим такой ответ: x e(-беск.,1)
Число 59 по условию это число равно: 5х+4=6у+5 5х-6у=5-4 5х-6у=1 5х=6у+1 5х - это число,делящееся на 5, кроме того за минусом 1, делящееся на 6 Подбираем числа делящиеся на 5: 15=14+1, не подходит, т. к.14 не делится на 6 25=24+1, вроде подходит, 24 делится на 6. Делаем проверку далее по условию. 25+4=29. Если это задуманное число, то при делении на 3, дает в остатке2. Верно. Далее, при делении на 4 дает в остатке 3. Неверно. 30=29+1 - нет 35=34+1 - нет 40= 39+1- нет 45= 44+1 - нет 50= 49+1 - нет 55=54+1 - да. Тогда задуманное число 55+4=59. 59 при делении на 2 дает в остатке 1, при делении на 3 дает в остатке 2, при делении на 4 дает в остатке 3. Значит, оно.
Первое, что можем заметить, это то, что выражение под корнем больше/равно нулю. Также замечаем, что знаменатель в дробовом выражении не может равняться нулю (Это записывать не нужно, так как будет включаться в решение неравенства).
Решим неравенство:
Отсюда имеем решение (значит и область определения):
x∈( -∞ ;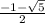 ) ∪ [ 0 ;
) ∪ [ 0 ; 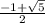 )
)